某同学在做“利用单摆测重力加速度”实验中,先测得摆线长为97.50cm,摆球直径为2.00cm,然后用秒表记录了单摆振动50次所用的时间为99.9s.则
①该摆摆长为_______cm。
②如果他测得的g值偏大,可能的原因是
| A.测摆线长时摆线拉的过紧 | B.摆球的质量测的不准确 |
| C.摆角太小,使周期变小 | D.实验中误将49次全振动数为50次 |
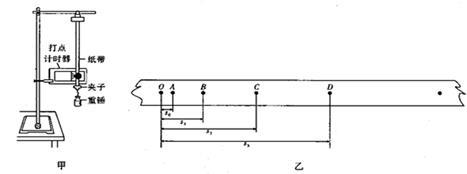
在“探究速度随时间变化的规律”实验中,小车做匀变速直线运动,记录小车运动的纸带如图所示.某同学在纸带上共选择7个计数点A、B、C、D、E、F、G,相邻两个计数点之间还有4个点没有画出.
(1)打点计时器是一种计时仪器,其电源频率为50Hz,常用的电磁式打点计时器和电火花计时器,使用的都是 (填“直流电”或“交流电”),它们是每隔 s打一个点.
(2)打B点时小车的速度vB= m/s,(要求保留两位有效数字)
(3)计算出小车运动的加速度为a= m/s2(要求保留两位有效数字)
用如图甲所示装置来探究功和动能变化的关系.木板上固定两个完全相同的遮光条A、B,用不可伸长的细线将木板通过两个滑轮与弹簧测力计C相连,木板放在安装有定滑轮和光电门的轨道D上,轨道放在水平桌面上,P为小桶(内有沙子),滑轮质量、摩擦不计,重力加速度g.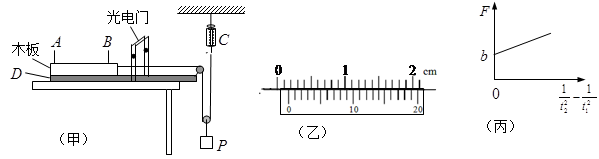
(1)实验中轨道应倾斜一定角度,这样做目的是 .
A.为了使释放木板后,木板能匀加速下滑
B.为了增大木板下滑的加速度
C.可使得细线拉力做的功等于合力对木板做的功
D.可使得木板在未施加拉力时能匀速下滑
(2)用游标卡尺测量遮光条的宽度,如图乙所示,则遮光条的宽度d= cm.
(3)实验主要步骤如下:
①测量木板、遮光条的总质量M,测量两遮光条的距离L;按甲图正确连接器材.
②将木板左端与轨道左端对齐,静止释放木板,木板在细线拉动下运动,记录弹簧测力计示数F及遮光条B、A先后经过光电门的时间为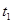 、
、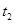 .则遮光条B、A通过光电门的过程中木板动能的变化量
.则遮光条B、A通过光电门的过程中木板动能的变化量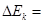 ,合外力对木板做功
,合外力对木板做功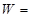 ,(用字母
,(用字母 表示).
表示).
③在小桶中增加沙子,重复②的操作.
④比较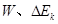 的大小,得出实验结论.
的大小,得出实验结论.
(4)若再本实验中轨道水平放置,其它条件和实验步骤不变,假设木板与轨道之间的动摩擦因数为 .测得多组
.测得多组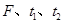 的数据,并得到F与
的数据,并得到F与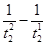 的关系图像如图丙.已知图像在纵轴上的截距为
的关系图像如图丙.已知图像在纵轴上的截距为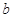 ,直线的斜率为
,直线的斜率为 ,求解
,求解 (用字母
(用字母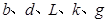 表示).
表示).
(1)关于“验证机械能守恒定律”的实验中,以下说法中正确的是
A.实验时需要称出重物的质量
B.实验中摩擦是不可避免的,因此纸带越短越好,因为纸带越短,克服摩擦做的功就少,误差就小
C.纸带上打下的第1、2点间距超过2mm,则无论怎样处理数据,实验误差都会很大
D.实验处理数据时,可直接利用打下的实际点迹,而不必采用“计数点”的方法
(2)若正确的操作完成实验,正确的选出纸带进行测量,量得连续三点A、B、C到第一个点O的距离如下图所示(相邻计数点时间间隔为0.02s),当地重力加速度的值为9.8m/s2,那么(结果均保留两位有效数字)
①纸带的 端与重物相连
②打下计数点B时,重物的速度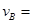 m/s
m/s
③在从起点O到打下计数点B的过程中,测得重物重力势能的减少量 略大于动能的增加量
略大于动能的增加量 ,这是因为 .
,这是因为 .
某同学利用图甲所示装置来探究平抛运动的规律,根据实验结果在坐标纸上描出了小球水平抛出后的运动轨迹,但不慎将画有轨迹图线的坐标纸损坏了一部分,剩余部分如图乙所示,P1、P2和P3是轨迹图线上的3个点,P1和P2、P2和P3之间的水平距离相等。设P1、P2和P3的横坐标分别为x1,x2和x3,纵坐标分别为y1、y2和y3,由图乙可侧出 ,
, ;
; 。若已知抛出后小球在水平方向做匀速运动,则小球从P1运动到P2所用的时间为 s,小球抛出后的水平速度为_m/s。(g取9.8 m/s2,结果保留2位有效数字)
。若已知抛出后小球在水平方向做匀速运动,则小球从P1运动到P2所用的时间为 s,小球抛出后的水平速度为_m/s。(g取9.8 m/s2,结果保留2位有效数字)
用如图甲所示的装置“验证机械能守恒定律”的实验中,打点计时器接在频率为f的交流电源上,从实验中打出的几条纸带中选出一条理想纸带,如图乙所示,从第一个点O开始选取纸带上打出的5个连续的点O、A、B、C、D,各点距起始点。的距离分别为s0、s1、s2、s3,已知重锤的质量为m,当地的重力加速度为g,则从打下起始点O到打下C点的过程中,重锤重力势能减少量的表达式为 ,重锤动能增加量的表达式为 。(均用题中所给字母表达)