用反证法证明命题“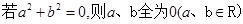 ”,其反设正确的是( )
”,其反设正确的是( )
A. |
B.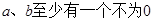 |
C. |
D. |
甲组有5名男同学,3名女同学;乙组有6名男同学、2名女同学。若从甲、乙两组中各选出2名同学,则选出的4人中恰有1名女同学的不同选法共有( )
| A.150种 | B.180种 | C.300种 | D.345种 |
下图a是某县参加2009年高考的学生身高条形统计图,从左到右的各条形表示的学生人数依次记为A1、A2、…、Am [如A2表示身高(单位:cm)在[150,155]内的学生人数]。图b是统计图a中身高在一定范围内学生人数的一个算法流程图。
现要统计身高在160~180cm(含160cm,不含180cm)的学生人数,那么在流程图中的判断框内应填写的条件是
A.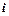 <9 <9 |
B.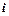 <8 <8 |
C.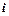 <7 <7 |
D.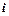 <6 <6 |
在古希腊毕达哥拉斯学派把1,3,6,10,15,21,28,…这些数叫做三角形数,因为这些数对应的点可以排成一个正三角形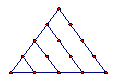
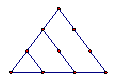
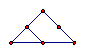
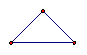

1 3 6 10 15
则第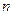 个三角形数为
个三角形数为
A.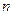 |
B.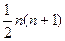 |
C.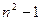 |
D.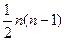 |
在区间[-1,1]上随机取一个数x,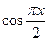 的值介于0到
的值介于0到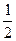 之间的概率为( ).
之间的概率为( ).
A.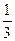 |
B.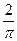 |
C.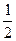 |
D.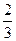 |
设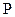 为曲线
为曲线 上的点,且曲线
上的点,且曲线 :
: 在点
在点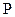 处切线倾斜角的取值范围为
处切线倾斜角的取值范围为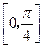 ,则点横坐标的取值范围为( )
,则点横坐标的取值范围为( )
A B
B 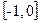 C
C  D
D