统计表明,某种型号的汽车在匀速行驶中每小时的耗油量 (升)关于行驶速度
(升)关于行驶速度 (千米/小时)的函数解析式可以表示为:
(千米/小时)的函数解析式可以表示为: 已知甲、乙两地相距100千米.
已知甲、乙两地相距100千米.
(1)当汽车以40千米/小时的速度匀速行驶时,从甲地到乙地要耗油多少升?
(2)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?
(本小题满分12分)
已知函数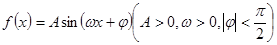 在一个周期内的部分函数图象如图所示,(I)求函数
在一个周期内的部分函数图象如图所示,(I)求函数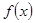 的解析式;(Ⅱ)求函数
的解析式;(Ⅱ)求函数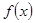 在区间
在区间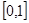 上的最大值和最小值.
上的最大值和最小值.
(本小题满分12分)
已知函数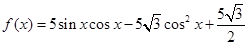 ,(Ⅰ)确定函数
,(Ⅰ)确定函数 的单调增区间;(Ⅱ)当函数
的单调增区间;(Ⅱ)当函数 取得最大值时,求自变量
取得最大值时,求自变量 的集合.
的集合.
(本小题满分12分)
已知|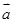 |=1,|
|=1,| |=
|= ;(I)若
;(I)若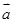 .
. =
=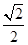 ,求
,求 与
与 的夹角;(II)若
的夹角;(II)若 与
与 的夹角为
的夹角为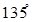 ,求|
,求|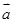 +
+ |.
|.
(本小题满分14分)已知函数 ,其中
,其中 .(1) 讨论函数
.(1) 讨论函数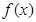 的单调性,并求出
的单调性,并求出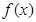 的极值;(2) 若对于任意
的极值;(2) 若对于任意 ,都存在
,都存在 ,使得
,使得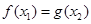 ,求实数
,求实数 的取值范围.
的取值范围.
(本小题满分13分)已知函数 (其中
(其中 且
且 为常数)的图像经过点A
为常数)的图像经过点A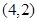 、B
、B .
. 是函数
是函数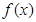 图像上的点,
图像上的点, 是
是 正半轴上的点.
正半轴上的点.
(1) 求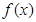 的解析式;
的解析式;
(2) 设 为坐标原点,
为坐标原点, 是一系列正三角形,记它们的边长是
是一系列正三角形,记它们的边长是 ,求数列
,求数列 的通项公式;
的通项公式;
(3) 在(2)的条件下,数列 满足
满足 ,记
,记 的前
的前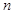 项和为
项和为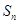 ,证明:
,证明: 。
。