2013年某工厂生产某种产品,每日的成本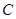 (单位:万元)与日产量
(单位:万元)与日产量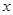 (单位:吨)满足函数关系式
(单位:吨)满足函数关系式 ,每日的销售额
,每日的销售额 (单位:万元)与日产量
(单位:万元)与日产量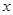 的函数关系式
的函数关系式
已知每日的利润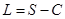 ,且当
,且当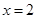 时,
时,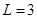 .
.
(1)求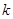 的值;
的值;
(2)当日产量为多少吨时,每日的利润可以达到最大,并求出最大值.
已知命题p: ,命题q:
,命题q: ,若
,若 与
与 都为假命题,求x的值。
都为假命题,求x的值。
(本小题满分12分)
已知点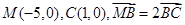 ,
,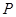 是平面上一动点,且满足
是平面上一动点,且满足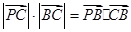 ,
,
(1)求点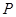 的轨迹
的轨迹 对应的方程;
对应的方程;
(2)已知点 在曲线
在曲线 上,过点
上,过点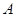 作曲线
作曲线 的两条弦
的两条弦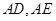 ,且
,且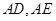 的斜率为
的斜率为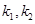 满足
满足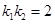 ,试判断动直线
,试判断动直线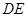 是否过定点,并证明你的结论.
是否过定点,并证明你的结论.
. (本小题满分12分)
已知函数 .
.
(1)若函数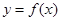 在
在 处取得极值,且曲线
处取得极值,且曲线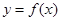 在点
在点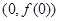 处的切线与直线
处的切线与直线 平行,求
平行,求 和
和 的值;
的值;
(2)若 ,试讨论函数
,试讨论函数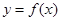 的单调性.
的单调性.
(本小题满分12分)
已知等差数列 满足:
满足: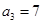 ,
, ,
, 的前n项和为
的前n项和为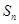 .
.
(Ⅰ)求通项公式 及前n项和
及前n项和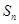 ;
;
(Ⅱ)令 =
= (n
(n N*),求数列
N*),求数列 的前n项和
的前n项和 .
.
(本小题满分12分)
已知四棱锥 的底面为直角梯形,
的底面为直角梯形, ∥
∥ ,∠
,∠ ,
, ⊥底面
⊥底面 ,且
,且 ,
, 是
是 的中点.
的中点.
(1)证明:平面 ⊥平面
⊥平面 ;
;
(2)求 与
与 所成角的余弦值;
所成角的余弦值;
(3)求二面角 的余弦值.
的余弦值.