已知关于x的一元二次函数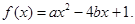
(1)设集合P={1,2,3}和Q={-1,1,2,3,4},分别从集合P和Q中随机取一个数作为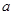 和
和 ,
,
求函数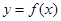 在区间[
在区间[ 上是增函数的概率;
上是增函数的概率;
(2)设点(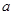 ,
, )是区域
)是区域 内的随机点,求函数
内的随机点,求函数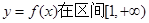 上是增函数的概率.
上是增函数的概率.
(本小题满分12分)已知函数 ,
, .
.
(1)当 时,求曲线
时,求曲线 在
在 处的切线方程;
处的切线方程;
(2)设函数 ,求函数
,求函数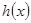 的单调区间;
的单调区间;
(3)若在 上存在一点
上存在一点 ,使得
,使得 成立,求
成立,求 的取值范围
的取值范围
(本小题满分12分)已知抛物线 ,直线
,直线 与抛物线交于
与抛物线交于 两点.
两点.
(1)若 轴与以
轴与以 为直径的圆相切,求该圆的方程;
为直径的圆相切,求该圆的方程;
(2)若直线与 轴负半轴相交,求
轴负半轴相交,求 面积的最大值
面积的最大值
(本小题满分12分)已知四棱锥 中,
中, 平面
平面 ,底面
,底面 是边长为
是边长为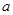 的菱形,
的菱形, ,
, .
.
(1)求证:平面 平面
平面 ;
;
(2)设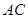 与
与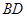 交于点
交于点 ,
, 为
为 中点,若二面角
中点,若二面角 的正切值为
的正切值为 ,
,
求 的值.
的值.
(本小题满分12分)某中学随机抽取部分高一学生调查其上学路上所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中上学路上所需时间的范围是 ,样本数据分组为
,样本数据分组为 ,
, ,
, ,
, ,
, .
.
(1)求直方图中 的值;
的值;
(2)如果上学路上所需时间不少于小时的学生可申请在学校住宿,若招生 名,请估计新生中有多少名学生可以申请住宿;
名,请估计新生中有多少名学生可以申请住宿;
(3)从学校的高一学生中任选4名学生,这4名学生中上学路上所需时间少于20分钟的人数记为 ,求
,求 的分布列和数学期望.(以直方图中的频率作为概率).
的分布列和数学期望.(以直方图中的频率作为概率).
(本小题满分12分)已知函数 满足
满足
(1)求实数 的值以及函数
的值以及函数 的最小正周期;
的最小正周期;
(2)记 ,若函数
,若函数 是偶函数,求实数
是偶函数,求实数 的值.
的值.