如图，CD=BE，DG⊥BC，EF⊥BC，垂足分别为G，F，且DG=EF。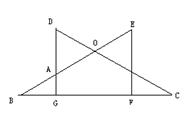
（1）
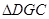与
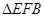全等吗？请说明理由；
（2）OB=OC吗？请说明理由；
（3）若∠B=30°，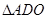
的形状是
阅读解答题：在数学中，有些大数值问题可以通过用字母代替数转化成整式问题来解决．例：若x=123456789×123456786，y=123456788×123456787，试比较x、y的大小．
解：设123456788=a，那么x=(a+1)(a－2)=a2－a－2，y=a(a－1)=a2－a，
∵x-y=(a2－a－2)－(a2－a)=－2＜0，∴x＜y．
这种方法不仅可以比大小，也能解计算．
看完后，你体会到了这种方法吗？不妨尝试一下，相信你准行！
问题：计算2×2.456×3.456－5.456×1.456－2.4562的值．
如图，五边形ABCDE中，AE∥BC，EF平分∠AED，CF平分∠BCD，
若∠EDC=75°，求∠EFC的度数．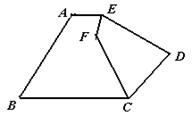
先化简， (x－1)(x－2)+3x(x+3)－4(x+2)(x－3)，再选择一个你喜欢的数，代入x后求值．
如图，DH交BF于点E，CH交BF于点G，∠1=∠2，∠3=∠4，∠B=∠5．
试判断CH和DF的位置关系并说明理由．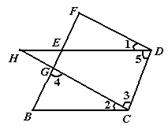
因式分解：
⑴ 3x2－27
⑵x3－6x2+9x
⑶ (x2+4)2－16x2．