我市某镇组织20辆汽车装运完A、B、C三种脐橙共100吨到外地销售。按计划，20辆汽车都要装运，每辆汽车只能装运同一种脐橙，且必须装满。根据下表提供的信息，解答以下问题：
| 脐 橙 品 种 |
A |
B |
C |
| 每辆汽车运载量（吨） |
6 |
5 |
4 |
| 每吨脐橙获得（百元） |
12 |
16 |
10 |
（1）设装运A种脐橙的车辆数为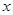
，装运B种脐橙的车辆数为
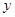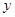，求与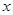之间的函数关系式；
（2）如果装运每种脐橙的车辆数都不少于4辆，那么车辆的安排方案有几种？并写出每种安排方案；
（3）若要使此次销售获利最大，应采用哪种安排方案？并求出最大利润的值。
在△ABC中，CG是∠ACB的角平分线，点D在BC上，且∠DAC＝∠B，CG和AD交于点F．
（1）求证：AG＝AF（如图1）；
（2）如图2，过点G作GE∥AD交BC于点E，连接EF，求证：EF∥AB．
如图，在△ABC中，∠C=90°，AD平分∠CAB，交CB于点D，过点D作DE⊥AB于点E．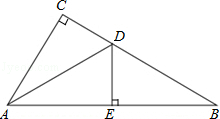
（1）求证：△ACD≌△AED；
（2）若∠B=30°，CD=1，求BD的长．
如图，△ABC 中，BD、CE分别是AC、AB上的高，BD与CE交于点O．BD=CE
（1）问△ABC为等腰三角形吗？为什么？
（2）问点O在∠A的平分线上吗？为什么？
如图，△ABC中，点D在边AB上，AC＝BC＝BD，AD＝CD，求∠A的度数．
如图，已知△ABC各顶点的坐标分别为A（－3，2），B（－4，－3），C（－1，－1），请你画出△ABC关于y轴对称的△A1B1C1，并写出△A1B1C1的各点坐标．