某校对高三年级800名男生的身高(单位:cm)进行了统计,随机抽取的一个容量为50的样本的频率分布直方图的部分图形如图所示,已知第一组与第八组人数相同,第六组、第七组、第八组人数依次构成等差数列.
(1)估计这所学校高三年级全体男生身高180 cm以上(含180 cm)的人数;
(2)求第六组、第七组的频率并补充完整频率分布直方图;
(3)若从身高属于第六组和第八组的所有男生中随机抽取两名男生,记他们的身高分别为x、y,求满足|x-y|≤5的事件概率.
如图,四棱锥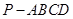 中,
中,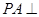 面
面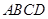 ,底面
,底面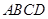 为矩形,
为矩形, 分别是
分别是 的中点,
的中点, ,
,
(1)求证: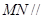 面
面 ;
;
(2)求证: 面
面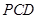 ;
;
(3)求四棱锥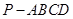 的表面积。
的表面积。
随机抽取某中学甲、乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图
(1)根据茎叶图判断哪个班的平均身高较高;
(2)求甲班的样本数据的中位数;
(3)现从乙班身高不低于170cm的同学中随机抽取两名,求身高为173cm的同学被抽中的概率.
为了解某市开展群众体育活动的情况,拟采用分层抽样的方法从 三个区中抽取
三个区中抽取 个工厂进行调查,已知
个工厂进行调查,已知 区中分别有
区中分别有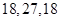 个工厂
个工厂
(1)求从 区中应分别抽取的工厂个数;
区中应分别抽取的工厂个数;
(2)若从抽得的 个工厂中随机地抽取
个工厂中随机地抽取 个进行调查结果的对比,计算这
个进行调查结果的对比,计算这 个工厂中至少有一个来自
个工厂中至少有一个来自 区的概率。
区的概率。
如图,在直三棱柱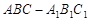 中,
中,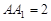 ,
, ,
, ,点
,点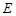 是
是 的中点,点
的中点,点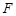 在侧棱
在侧棱 上,且
上,且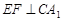 .
.
(1)求二面角
 的大小;
的大小;
(2)求点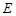 到平面
到平面 的距离.
的距离.