已知矩形纸片ABCD中，AB＝2，BC＝3．
操作：将矩形纸片沿EF折叠，使点B落在边CD上．
探究：
（1）如图1，若点B与点D重合，你认为△EDA1和△FDC全等吗？如果全等，请给出证明，如果不全等，请说明理由；
（2）如图2，若点B与CD的中点重合，请你判断△FCB1、△B1DG和△EA1G之间的关系，如果全等，只需写出结果，如果相似，请写出结果和相应的相似比；
（3）如图2，请你探索，当点B落在CD边上何处，即B1C的长度为多少时，△FCB1与△B1DG全等．
如图，⊙O的半径为1，点P是⊙O上一点，弦AB垂直平分线段OP，点D是APB上任一点（与端点A、B不重合），DE⊥AB于点E，以点D为圆心、DE长为半径作⊙D，分别过点A、B作⊙D的切线，两条切线相交于点C．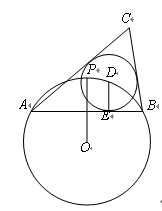
（1）求弦AB的长；
（2）判断∠ACB是否为定值，若是，求出∠ACB的大小；否则，请说明理由；
（3）记△ABC的面积为S，若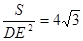
，求△ABC的周长.
如图，已知PA、PB切⊙O于A、B两点，连AB，且PA，PB的长是方程
＝ 0的两根，AB =" m." 试求：
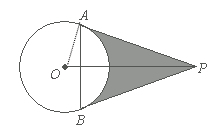
(1)⊙O的半径；(2)由PA，PB，围成图形(即阴影部分)的面积. （计算结果用含有π的式子表示）
如图，⊙O的直径AB=4，∠ABC=30°，BC=4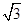
，D是线段BC的中点。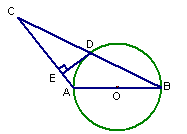
（1）试判断点D与⊙O的位置关系，并说明理由；
（2）过点D作DE⊥AC，垂足为点E，求证：直线DE是⊙O的切线。
若关于x的方程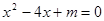
．
（1）方程有两个不相等的实数根，求实数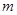
的取值范围．
（2）若方程的一个根是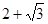
，求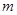的值及另一个根．
如图所示，AB是⊙O的一条弦，OD⊥AB，垂足为Ｃ，交⊙O于点D，点Ｅ在⊙O上。
（1）若
，求
的度数；
（2）若
，
，求
的长．