如图:已知AB∥DE∥CF,若∠ABC=60°,∠CDE=140°,求∠BCD的度数。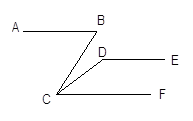
已知A、B在数轴上分别表示a,b.
(1)对照数轴填写下表:
(2)若A、B两点间的距离记为d,试问:d和a,b有何数量关系?
(3)在数轴上标出所有符合条件的整数点P,使它到10和-10的距离之和为20,并求所有这些整数的和;
(4)找出(3)中满足到10和-10的距离之差大于1而小于5的整数的点P;
(5)若点C表示的数为x,当点C在什么位置时,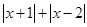 取得的值最小?
取得的值最小?
如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动。它从A处出发去看望B、C、D处的其它甲虫,规定:向上向右走为正,向下向左走为负。如果从A到B记为:A→B(+l,+3);从C到D记为:C→D(+1,-2)。其中第一个数表示左右方向,第二个数表示上下方向,那么图中

(1)A→C(,),C→(-2,);
(2)若这只甲虫的行走路线为A→B→C→D,请计算该甲虫走过的路程;
(3)假如这只甲虫从A处去甲虫P处的行走路线依次为(+2,+2),(+1,-1),(-2,+3),请在图中标出P的位置。
根据某地实验测得的数据表明,高度每增加1 km,气温大约下降6℃,已知该地地面温度为21℃.
(1)高空某处高度是8 km,求此处的温度是多少;
(2)高空某处温度为一24 ℃,求此处的高度.
2009年3月17日俄罗斯特技飞行队在名胜风景旅游区——张家界天门洞特技表演,其中一架飞机起飞后的高度变化如下表:
(1)此时这架飞机比起飞点高了多少千米?
(2)如果飞机每上升或下降1 km需消耗2L燃油,那么这架飞机在这4个动作表演过程中,一共消耗了多少升燃油?
(3)如果飞机做特技表演时,有4个规定动作,前3个动作起飞后高度变化如下:上升3.8km,下降2.9km,再上升1.6km,若要使飞机最终比起飞点高出1km,问第4个动作是上升还是下降,上升或下降多少千米?
学校图书馆上周借书记录如下(超过50册的部分记为正,少于50册的部分记为负):
(1)上星期五借出图书________册.
(2)上星期二比上星期五多借出图书________册。
(3)上周平均每天借出图书多少册?(一周以5天计算)