如图,方格纸中每个小方格都是边长为1个单位长度的正方形,已知点A(-1,1),现将A点先向左平移3个单位,再向下平移4个单位得到点B,然后作点B关于 轴的对称点得到C点,最后做点C关于
轴的对称点得到C点,最后做点C关于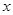 轴的对称点得到D点。
轴的对称点得到D点。
在坐标系中作出点A、B、C、D。
顺次连接ABCDA,求四边形ABCD的面积。
已知:如图,四边形ABCD中,BC=CD=DB,∠ADB=90°,sin∠ABD= ,S△BCD=
,S△BCD=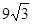 . 求四边形ABCD的周长.
. 求四边形ABCD的周长.
某中学库存960套旧桌凳,修理后捐助贫困山区学校.现有甲、乙两个木工小组都想承揽这项业务.经协商后得知:甲小组单独修理这批桌凳比乙小组多用20天;乙小组每天修的桌凳套数是甲小组的1.5倍.求甲、乙两个木工小组每天各修桌凳多少套?
如图,已知反比例函数y=  (x>0)的图象与一次函数y=kx+b的图象交于点A(1,m),B(n,2)两点.
(x>0)的图象与一次函数y=kx+b的图象交于点A(1,m),B(n,2)两点.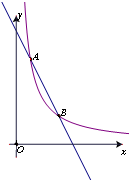
求一次函数的解析式
结合图象回答:反比例函数的值大于一次函数的值时x的取值范围.
已知:如图,点E、F分别为□ABCD 的BC、AD边上的点,且∠1="∠2." 求证:AE="FC." 
已知: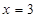 ,求
,求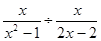 的值.
的值.