已知:如图,在△ABC中,BC=AC,以BC为直径的⊙O与边AB相交于点D,DE⊥AC,垂足为点E.
(1)求证:点D是AB的中点;
(2)判断DE与⊙O的位置关系,并证明你的结论;
(3)若⊙O的直径为18,cosB= ,求DE的长.
,求DE的长.
已知⊙O的半径为13cm,弦AB∥CD,AB=24cm,CD=10cm,求AB和CD之间的距离.
已知BD垂直平分AC,∠BCD=∠ADF,AF⊥AC,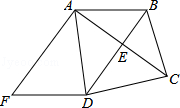
(1)证明四边形ABDF是平行四边形;
(2)若AF=DF=5,AD=6,求AC的长.
如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF.
(1)试说明AC=EF;
(2)求证:四边形ADFE是平行四边形.
前夕,某商店根据市场调查,用3000元购进第一批盒装花,上市后很快售完,接着又用5000元购进第二批这种盒装花.已知第二批所购花的盒数是第一批所购花盒数的2倍,且每盒花的进价比第一批的进价少5元.求第一批盒装花每盒的进价是多少元?
因式分解:
(1)4a2b2﹣(a2+b2)2;
(2)(a+x)4﹣(a﹣x)4.
(3)分解因式:(x﹣y)2﹣4(x﹣y﹣1)
(4)a2﹣4ax+4a;
(5)(x2﹣1)2+6(1﹣x2)+9.