如图 ,在平面直角坐标系中,等腰直角
,在平面直角坐标系中,等腰直角 的斜边
的斜边 在
在 轴上,顶点
轴上,顶点 的坐标为
的坐标为 ,
, 为斜边上的高.抛物线
为斜边上的高.抛物线 与直线
与直线 交于点
交于点 ,点
,点 的横坐标为
的横坐标为 .点
.点 在
在 轴的正半轴上,过点
轴的正半轴上,过点 作
作 轴.交射线
轴.交射线 于点
于点 .设点
.设点 的横坐标为
的横坐标为 ,以
,以 为顶点的四边形的面积为
为顶点的四边形的面积为 .
.
(1)求 所在直线的解析式;
所在直线的解析式;
(2)求 的值;
的值;
(3)当 时,求
时,求 与
与 的函数关系式;
的函数关系式;
(4)如图 ,设直线
,设直线 交射线
交射线 于点
于点 ,交抛物线于点
,交抛物线于点 .以
.以 为一边,在
为一边,在 的右侧作矩形
的右侧作矩形 ,其中
,其中 .直接写出矩形
.直接写出矩形 与
与 重叠部分为轴对称图形时
重叠部分为轴对称图形时 的取值范围.
的取值范围.
某文化用品商店用2000元购进一批学生书包,面市后发现供不应求,商店又购进第二批同样的书包,所购数量是第一批购进数量的3倍,但单价贵了4元,结果第二批用了6300元。(1)求第一批购进书包的单价是多少元?(2)若商店销售这两批书包时,每个售价都是120元,全部售出后,商店共盈利多少元?
在⊿ABC中,AB=AC,D为BC中点,四边形ABDE是平行四边形,求证:四边形ADCE是矩形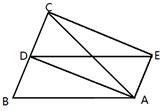
折叠矩形ABCD的一边AD, 折痕为AE, 且使点D落在BC边上的点F处,已知AB=8cm,BC=10cm,以B点为原点,BC为x轴,BA为y轴建立平面直角坐标系。求点F和点E坐标。
如图,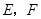 是平行四边形
是平行四边形 的对角线
的对角线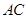 上的点,
上的点, .请你猜想:
.请你猜想: 与
与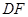 有怎样的位置关系和数量关系?并对你的猜想加以证明:
有怎样的位置关系和数量关系?并对你的猜想加以证明:
已知一次函数y=ax+b的图像与反比例函数 的图像交于A(2,2),B(-1,m),求反比例函数和一次函数的解析式.
的图像交于A(2,2),B(-1,m),求反比例函数和一次函数的解析式.