如图,已知二次函数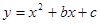
的图象与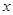
轴交于A、B两点，与
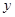轴交于点P，顶点为C（1，-2）.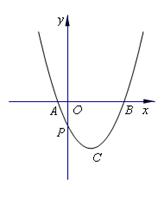
（1)求此函数的关系式；
（2)作点C关于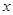轴的对称点D，顺次连接A、C、B、D.若在抛物线上存在点E，使直线PE将四边形ABCD分成面积相等的两个四边形，求点E的坐标；
（3）在（2）的条件下，抛物线上是否存在一点F，使得△PEF是以P为直角顶点的直角三角形？若存在，求出点F的坐标及△PEF的面积；若不存在，请说明理由.
如图，某玩具是由两个正方体用胶水黏合而成的，它们的棱长分别为1dm和2dm，为了美观，现要在其表面喷涂油漆，已知喷涂1dm2需用油漆59克，求喷涂这个玩具共需多少克油漆？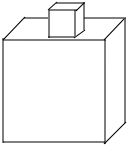
在计算器上，按照下面的程序进行操作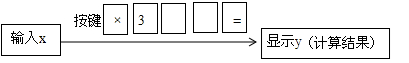
下表中的x与y分别是输入的6个数及相应的计算结果：上面操作程序中所按的第三个键和第四个键应是______．
| x |
﹣2 |
﹣1 |
0 |
1 |
2 |
3 |
| y |
﹣5 |
﹣2 |
1 |
4 |
7 |
10 |
（1）计算下列各题：
①22×32与（2×3）2；
②（﹣2）4×34与（﹣2×3）4；
③27×2与28．
（2）比较（1）中的结果，由此可以推断an×bn______（a×b）n，an+1_______an×a．
（3）试根据（2）的结论，不用计算器计算0.1252010×82011的值．
用计算器计算（写出按键顺序）．
（1）（﹣15）3÷52
（2）﹣10+8÷22﹣（﹣4）×（﹣3）．
有一张厚度是0.1mm的纸，假设我们能将它连续对折30次，这时它的厚度能超过珠穆朗玛峰的海拔高度（8845米）吗？请用计数器帮你得出答案．