(文科只做(1)(2)问,理科全做)
设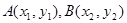 是函数
是函数 图象上任意两点,且
图象上任意两点,且 ,已知点
,已知点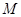 的横坐标为
的横坐标为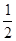 ,且有
,且有 ,其中
,其中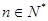 且n≥2,
且n≥2,
(1) 求点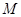 的纵坐标值;
的纵坐标值;
(2) 求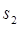 ,
,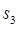 ,
,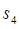 及
及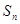 ;
;
(3)已知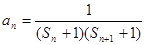 ,其中
,其中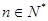 ,且
,且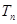 为数列
为数列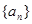 的前n项和,若
的前n项和,若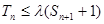 对一切
对一切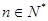 都成立,试求λ的最小正整数值。
都成立,试求λ的最小正整数值。
(本小题满分14分)设甲、乙两套试验方案在一次试验中成功的概率均为p,且这两套试验方案中至少有一套试验成功的概率为0.51,假设这两套试验方案在试验过程中,相互之间没有影响.,设试验成功的方案的个数为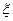 .(Ⅰ)求p的值;(Ⅱ)求
.(Ⅰ)求p的值;(Ⅱ)求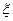 的数学期望E
的数学期望E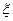 与方差D
与方差D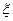 .
.
(本小题满分14分)设数列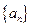 的前项和为
的前项和为 ,且
,且
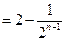 ,
, 为等差数列,且
为等差数列,且 ,
, .(Ⅰ)求数列
.(Ⅰ)求数列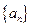 和
和 通项公式;(Ⅱ)设
通项公式;(Ⅱ)设 ,求数列
,求数列 的前
的前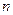 项和
项和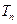 .
.
(本小题满分12分)盒中有6只灯泡,其中有2只是次品,4只是正品.从中任取2只,试求下列事件的概率. (Ⅰ)取到的2只都是次品;(Ⅱ)取到的2只中恰有一只次品.
如图, ,双曲线M是以B、C为焦点且过A点.(Ⅰ)建立适当的坐标系,求双曲线M的方程;(Ⅱ)设过点E(1,0)的直线l分别与双曲线M的左、右支交于F、G两点,直线l的斜率为k,求k的取值范围.;
,双曲线M是以B、C为焦点且过A点.(Ⅰ)建立适当的坐标系,求双曲线M的方程;(Ⅱ)设过点E(1,0)的直线l分别与双曲线M的左、右支交于F、G两点,直线l的斜率为k,求k的取值范围.;
(Ⅲ)对于(II)中的直线l,是否存在k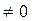 使|OF|=|OG|
使|OF|=|OG|
若有求出k的值,若没有说明理由.(O为原点)
(本题满分为14分)已知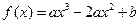 ,(
,(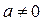 ).(Ⅰ)求出f(x)的极值点,并指出其是极大值点还是极小值点;(Ⅱ)若f(x)在区间
).(Ⅰ)求出f(x)的极值点,并指出其是极大值点还是极小值点;(Ⅱ)若f(x)在区间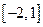 上最大值是5,最小值是-11,求
上最大值是5,最小值是-11,求 的解析式.
的解析式.