如图,在△ABC中,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且AC=CF,∠CBF=∠CFB.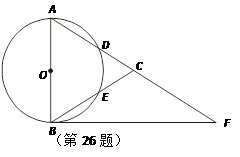
(1)求证:直线BF是⊙O的切线;
(2)若点D,点E分别是弧AB的三等分点,当AD=5时,求BF的长和扇形DOE的面积;
(3)在(2)的条件下,如果以点C为圆心,r为半径的圆上总存在不同的两点到点O的距离为5,则r的取值范围为 .
如图,在边长为1的小正方形组成的网格中,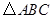 的三个顶点均在格点上,请按要求完成下列各题:
的三个顶点均在格点上,请按要求完成下列各题:
(1)用签字笔画AD∥BC(D为格点),连接CD;线段CD的长为;
(2)请你在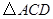 的三个内角中任选一个锐角,若你所选的锐角是,则它所对应的正弦函数值是.
的三个内角中任选一个锐角,若你所选的锐角是,则它所对应的正弦函数值是.
(3)若E为BC中点,则tan∠CAE的值是.
小明有2枚黑棋子,小亮有2枚白棋子,两人随机将4枚棋子放在下图的格子中(每格只放一枚)。若4枚棋子黑白相间排列,就算小明赢,否则就算小亮赢.这个游戏对双方公平吗?请说明理由.
“五一”期间,某超市贴出促销海报,内容如图1.在商场活动期间,王莉和同组同学随机调查了部分参与活动的顾客,统计了200人次的摸奖情况,绘制成如图2的频数分布直方图.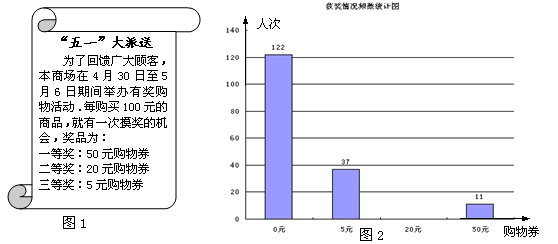
(1)补齐频数分布直方图;
(2)求所调查的200人次摸奖的获奖率;
(3)若超市每天约有2000人次摸奖,请估算商场一天送出的购物券总金额是多少元?
如图,在等腰梯形 中,
中,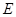 为底
为底 的中点,连结
的中点,连结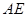 、
、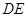 .
.
求证: .
.
已知二次函数y=x2+bx+c与x轴交于A(-1,0)、B(1,0)两点.
(1)求这个二次函数的关系式;
(2)若有一半径为r的⊙P,且圆心P在抛物线上运动,当⊙P与两坐标轴都相切时,求半径r的值.
(3)半径为1的⊙P在抛物线上,当点P的纵坐标在什么范围内取值时,⊙P与y轴相离、相交?