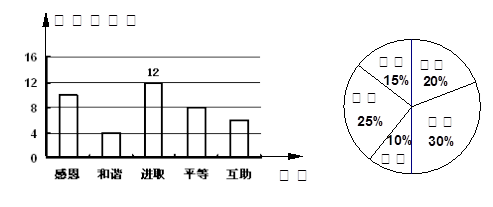
某校开展了以“责任、感恩”为主题的班队活动,活动结束后,初三(2)班数学兴趣小组提出了5个主要观点并在本班学生中进行了调查(要求每位同学只选自己最认可的一项观点),并制成了如下扇形统计图,该班有 ▲ 人,学生选择“和谐”观点的有___▲____人,在扇形统计图中,“和谐”观点所在扇形区域的圆心角是___▲____度;
如果该校有360名初三学生,利用样本估计选择“感恩”观点的初三学生约有_▲_人;
如果数学兴趣小组在这5个主要观点中任选两项观点在全校学生中进行调查,求恰好选到“和谐”和“感恩”观点的概率(用树状图或列表法分析解答).
(本题10分)已知反比例函数y= (m为常数)的图
(m为常数)的图
象经过点A(-1,6).
(1)求m的值;
(2)如图,过点A作直线AC与函数y= 的图象交于点
的图象交于点
B,与x轴交于点C,且AB=2BC,求点C的坐标.
(本题10分)腾飞中学在教学楼前新建了一座“腾飞”雕塑(如图①).为了测量雕塑的高度,小明在二楼找到一点C,利用三角板测得雕塑顶端A点的仰角为 ,底部B点的俯角为
,底部B点的俯角为 ,小华在五楼找到一点D,利用三角板测得A点的俯角为
,小华在五楼找到一点D,利用三角板测得A点的俯角为 (如图②).若已知CD为12米,请求出雕塑AB的高度.(结果精确到0.1米,参考数据
(如图②).若已知CD为12米,请求出雕塑AB的高度.(结果精确到0.1米,参考数据 ).
).
(本题8分)某中学开展演讲比赛活动,九(1)、九(2)班根据初赛成绩各选出5名选手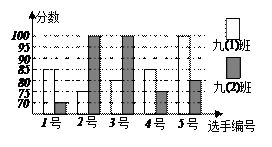
参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如下图所示.
(1)根据左图填写 下表
下表
| 平均分(分) |
中位数(分) |
众数(分) |
|
| 九(1)班 |
85 |
85 |
|
| 九(2)班 |
85 |
80 |
(2)结合两班复赛成绩的平均数和中位数,分析哪
个班级的复赛成绩较好?
(3)如果在每班参加复赛的选手中分别选出2人参
加决赛,你认为哪个班的实力更强一些,说明理由.
(本题8分)如图,四边形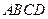 中,
中,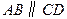 ,
,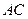 平分
平分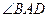 ,
,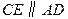 交
交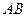 于
于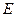 .
.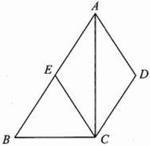
(1)求证:四边形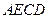 是菱形;
是菱形;
(2)若点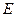 是
是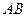 的中点,试判断
的中点,试判断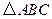 的形状,并说明理由.
的形状,并说明理由.
学了《认识事件的可能性》,林林想到了小时候常玩“锤子、剪刀、布”,他想两个人一起玩,有哪些可能情况?请你用列表的方式帮他写出来