已知，矩形ABCD中，AB=4cm，BC=8cm，AC的垂直平分线EF分别交AD、BC于点E、F，垂足为O．
（1）如图1，连接AF、CE．求证四边形AFCE为菱形，并求AF的长；
（2）如图2，动点P、Q分别从A、C两点同时出发，沿△AFB和△CDE各边匀速运动一周．即点P自A→F→B→A停止，点Q自C→D→E→C停止．在运动过程中，
①已知点P的速度为每秒5cm，点Q的速度为每秒4cm，运动时间为t秒，当A、C、P、Q四点为顶点的四边形是平行四边形时，求t的值．
②若点P、Q的运动路程分别为a、b（单位：cm，ab≠0），已知A、C、P、Q四点为顶点的四边形是平行四边形，求a与b满足的数量关系式．
（每小题4分，共8分）
（1）解方程：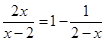
；
（2）解不等式组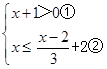
，并写出最小整数解
（每小题4分，共8分）
（1）计算：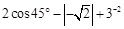
（2）化简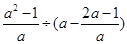
在平面直角坐标系xOy中，已知二次函数的图像经过原点及点A（1,2）与x轴相交于另一点B(3,0)，将点B向右平移3个单位得点C．
(1)求二次函数的解析式；
(2)点M在线段OC上，平面内有一点Q，使得四边形ABMQ为菱形，求点M坐标；
(3)点P在线段OC上，从O点出发向C点运动，过P点作x轴的垂线，交直线AO于D点，以PD为边在PD的右侧作正方形PDEF（当P点运动时，点D、点E、点F也随之运动）；
①当点E在二次函数的图像上时，求OP的长；
②若点P从O点出发向C点做匀速运动，速度为每秒1个单位长度，若P点运动t秒时，直线AC与以DE为直径的⊙M相切，直接写出此刻t的值．
如图，在Rt△ABC中，∠C=90°，AB=10cm,BC=6cm，点P、Q同时从点C出发，分别沿C→A和 C→B的方向运动，速度分别为2cm/s和1cm/s.过点P作PM⊥AC交AB于M，分别连接PQ、PM．当点Q运动到B时，两点都停止．设运动时间为t秒．
(1)当t=s时，PQ⊥QM？
(2)将△PQM沿PM翻折，得到△PMQ/．
①当t=s时,点Q/恰好落在AB上；
②设△PMQ/与△ABC重叠部分的面积为Scm2，求：S与t的函数关系式，并指出t的取值范围．
如图，四边形ABCD是正方形，△ABE是等边三角形，M为对角线BD（不含B点）上任意一点，将BM绕点B逆时针旋转60°得到BN，连接EN、AM、CM.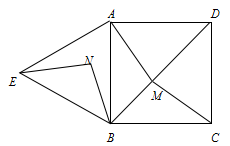
(1)求证：△AMB≌△ENB；
(2)①当M点在__________时，AM＋CM的值最小；②当M点在何处时，AM＋BM＋CM的值最小，并说明理由；
(3)当AM＋BM＋CM的最小值为
时，求正方形的边长.