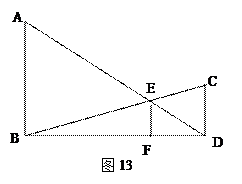如图,在Rt△ABC中,∠C=90°,AB=10cm,BC=6cm,点P、Q同时从点C出发,分别沿C→A和 C→B的方向运动,速度分别为2cm/s和1cm/s.过点P作PM⊥AC交AB于M,分别连接PQ、PM.当点Q运动到B时,两点都停止.设运动时间为t秒.
(1)当t= s时,PQ⊥QM?
(2)将△PQM沿PM翻折,得到△PMQ/.
①当t= s时,点Q/恰好落在AB上;
②设△PMQ/与△ABC重叠部分的面积为Scm2,求:S与t的函数关系式,并指出t的取值范围.
(本题满分5分)写出二次函数y=-x2-4x-6的图象的顶点坐标和对称轴的位置,并求出它的最大值或最小值.
(本题满分5分)如图,已知在Rt△ABC中,∠C=90°,BC=1,AC=2,
求tan A和sin B的值.
(本题满分5分)解方程:(x+1)(x-2)=x+1.
若矩形的一个短边与长边的比值为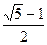 ,(黄金分割数),我们把这样的矩形叫做黄金矩形
,(黄金分割数),我们把这样的矩形叫做黄金矩形
(1)操作:请你在如图15所示的黄金矩形ABCD(AB>AD)中,以短边AD为一边作正方形AEFD。
(2)探究:在(1)中的四边形EBCF是不是黄金矩形?若是,请予以证明;若不是,请说明理由。
(3)归纳:通过上述操作及探究,请概括出具体有一般性的结论(不需证明)
已知,如图13,AB⊥BD,CD⊥BD,垂足分别为B、D,AD和BC交于点E,EF⊥BD,垂足为F,我们可以证明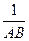 +
+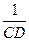 =
=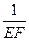 成立,若将图13中的垂直改为斜交,如图14,AB∥CD,AB与BC交于点E,过点E作EF∥AB交BD于F,则
成立,若将图13中的垂直改为斜交,如图14,AB∥CD,AB与BC交于点E,过点E作EF∥AB交BD于F,则
(1)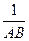 +
+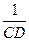 =
=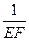 还成立吗?如果成立,给出证明;如果不成立,请说明理由。
还成立吗?如果成立,给出证明;如果不成立,请说明理由。
(2)请找出S△ABC,S△BED和S△BDC间的关系,并给出证明。