不等式选讲
设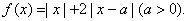
(1)当a=l时,解不等式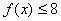 ;
;
(2)若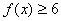 恒成立,求正实数a的取值范围。
恒成立,求正实数a的取值范围。
(本小题满分10分)设集合 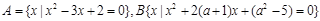
(1)若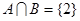 ,求实数a的值;
,求实数a的值;
(2)若 ,求实数a的取值范围。
,求实数a的取值范围。
(本小题满分14分)已知函数 (Ⅰ)当
(Ⅰ)当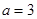 时,求
时,求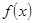 的单调增区间;(Ⅱ)若
的单调增区间;(Ⅱ)若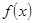 在
在 上是增函数,求
上是增函数,求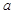 得取值范围;(Ⅲ)
得取值范围;(Ⅲ) 在(Ⅱ)的结论下,设
在(Ⅱ)的结论下,设 ,求函数
,求函数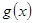 的最小值.
的最小值.
(本小题满分13分)已知椭圆C的中心在坐标原点,离心率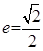 ,且其中一个焦点与抛物线
,且其中一个焦点与抛物线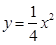 的焦点重合.(Ⅰ)求椭圆C的方程;(Ⅱ)过点
的焦点重合.(Ⅰ)求椭圆C的方程;(Ⅱ)过点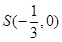 的动直线l交椭圆C于A、B两点,试问:在坐标平面上是否存在一个定点T,使得无论l如何转动,以AB为直径的圆恒过点T,若存在,求出点T的坐标;若不存在,请说明理由.
的动直线l交椭圆C于A、B两点,试问:在坐标平面上是否存在一个定点T,使得无论l如何转动,以AB为直径的圆恒过点T,若存在,求出点T的坐标;若不存在,请说明理由.
(本小题满分12分)某企业准备招聘一批大学生到本单位就业,但在签约前要对他们的某项专业技能进行测试.在待测试的某一个小组中有男、女生共10人(其中女生人数多于男生人数),如果从中随机选2人参加测试,其中恰为一男一女的概率为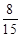 ;(Ⅰ)求该小组中女生的人数;(Ⅱ)假设此项专业技能测试对该小组的学生而言,每个女生通过的概率均为
;(Ⅰ)求该小组中女生的人数;(Ⅱ)假设此项专业技能测试对该小组的学生而言,每个女生通过的概率均为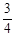 ,每个男生通过的概率均为
,每个男生通过的概率均为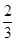 ;现对该小组中男生甲、男生乙和女生丙3个人进行测试,记这3人中通过测试的人数为随机变量
;现对该小组中男生甲、男生乙和女生丙3个人进行测试,记这3人中通过测试的人数为随机变量 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
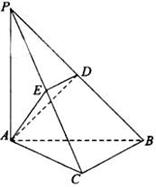
(本小题满分12分)如图,在三棱锥 中,
中,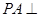 底面
底面 ,
,
点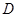 ,
,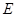 分别在棱
分别在棱 上,且
上,且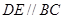
(Ⅰ)求证: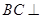 平面
平面 ;
;
(Ⅱ)当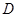 为
为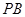 的中点时,求
的中点时,求 与平面
与平面 所成的角的余弦值;
所成的角的余弦值;
(Ⅲ)是否存在点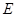 使得二面角
使得二面角 为直二面角?并说明理由.
为直二面角?并说明理由.