某商家举办购物抽奖活动,盒中有大小相同的9张卡片,其中三张标有数字1,两张标有数字0,四张标有数字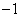 ,先从中任取三张卡片,将卡片上的数字相加,设数字和为
,先从中任取三张卡片,将卡片上的数字相加,设数字和为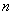 ,当
,当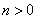 时,奖励奖金
时,奖励奖金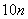 元;当
元;当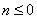 时,无奖励.
时,无奖励.
(1)求取出的三个数字中恰有一个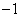 的概率.
的概率.
(2)设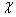 为奖金金额,求
为奖金金额,求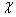 的分布列和期望.
的分布列和期望.
定义在 上的函数
上的函数 ,如果满足:对任意
,如果满足:对任意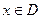 ,存在常数
,存在常数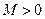 ,都有
,都有 成立,则称
成立,则称 是
是 上的有界函数,其中
上的有界函数,其中 称为函数
称为函数 的上界.
的上界.
已知函数 .
.
(1)当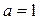 时,求函数
时,求函数 在
在 上的值域,并判断函数
上的值域,并判断函数 在
在 上是否为有界函数,请说明理由;
上是否为有界函数,请说明理由;
(2)若函数 在
在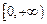 上是以3为上界的有界函数,求实数
上是以3为上界的有界函数,求实数 的取值范围.
的取值范围.
在直三棱柱 中,
中, ,
, 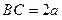 ,
, 是
是 的中点,
的中点, 是
是 上一点,且
上一点,且 .
.
(1)求证: 平面
平面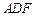 ;
;
(2)求三棱锥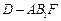 的体积;
的体积;
(3)试在 上找一点
上找一点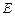 ,使得
,使得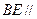 平面
平面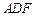 .
.
已知函数 ,常数
,常数 .
.
(1)讨论函数 的奇偶性,并说明理由;
的奇偶性,并说明理由;
(2)若函数 在
在 上为增函数,求
上为增函数,求 的取值范围
的取值范围
在平面直角坐标系 ,已知圆心在第二象限、半径为
,已知圆心在第二象限、半径为 的圆C与直线y=x相切于
的圆C与直线y=x相切于
坐标原点O.椭圆 与圆C的一个交点到椭圆两焦点的距离之和为
与圆C的一个交点到椭圆两焦点的距离之和为 .
.
(1)求圆C的方程;
(2)圆C上是否存在异于原点的点Q,使 (F为椭圆右焦点),若存在,请
(F为椭圆右焦点),若存在,请
求出点Q的坐标;若不存在,请说明理由.
设平面向量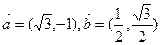 ,若存在实数
,若存在实数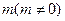 和角
和角 ,其中
,其中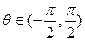 ,使向量
,使向量 ,且
,且 .
.
(1).求 的关系式;
的关系式;
(2).若 ,求
,求 的最小值,并求出此时的
的最小值,并求出此时的 值.
值.