如图,在四棱柱ABCD-A1B1C1D1中,D1D⊥底面ABCD,底面ABCD是正方形,且AB=1,D1D= .
.
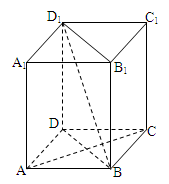
(1)求直线D1B与平面ABCD所成角的大小;
(2)求证:AC⊥平面BB1D1D.
(本小题满分14分)设数列{an}和{bn}满足a1=b1=6,a2=b2=4,a3=b3=3,且数列{an+1-an}是等差数列,数列{bn―2}是等比数列(n∈N*).
(Ⅰ)求数列{an},{bn}的通项公式;
(Ⅱ)是否存在k∈N*,使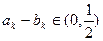 ?若存在,求出k,若不存在,说明理由.
?若存在,求出k,若不存在,说明理由.
(本小题满分14分)已知椭圆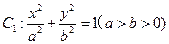 的右焦点为F,上顶点为A,P为C
的右焦点为F,上顶点为A,P为C 上任一点,MN是圆
上任一点,MN是圆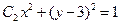 的一条直径,若与AF平行且在y轴上的截距为
的一条直径,若与AF平行且在y轴上的截距为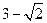 的直线
的直线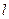 恰好与圆
恰好与圆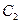 相切.
相切.
(Ⅰ)求椭圆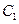 的离心率;
的离心率;
(Ⅱ)若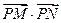 的最大值为49,求椭圆C
的最大值为49,求椭圆C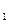 的方程.
的方程.
(本小题满分14分)已知
(Ⅰ)求 ;
;
(Ⅱ)若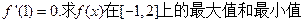 ;
;
(Ⅲ)若 <
<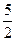 ,求证:当
,求证:当 和
和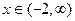 时,
时,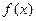 都是单调增函数.
都是单调增函数.
(本小题满分13分)如图,在三棱锥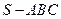 中,侧面
中,侧面 与侧面
与侧面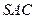 均为边长为1
均为边长为1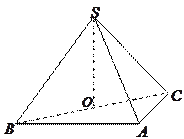
的等边三角形, ,
, 为
为 中点.
中点.
(Ⅰ)证明: 平面
平面 ;
;
(Ⅱ)证明: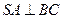 ;
;
(Ⅲ)求三棱锥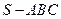 的体积.
的体积.
(本小题满分13分)甲、乙二人用4张扑克牌(分别是红心2、红心3、红心4、方块4)
玩游戏,他们将扑克牌洗匀后,背面朝上放在桌面上,甲先抽,乙后抽,抽出的牌不放回,
各抽一张.
(Ⅰ)写出甲、乙二人抽到的牌的所有基本事件; (Ⅱ)当甲抽到红心3时,求乙抽出的牌的牌面数字比3大的概率;
(Ⅱ)当甲抽到红心3时,求乙抽出的牌的牌面数字比3大的概率;
(Ⅲ)甲、乙约定:若甲抽到的牌的牌面数字比乙大,则甲胜;反之,则乙胜,你认为
此游戏是否公平说明你的理由.