已知函数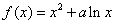
(Ⅰ)当a=﹣2时,求函数f(x)的单调区间;
(Ⅱ)若g(x)= 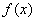 +
+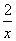 在
在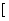 1,+∞)上是单调函数,求实数a的取值范围.
1,+∞)上是单调函数,求实数a的取值范围.
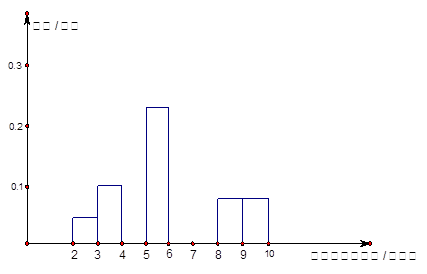
某市为了保障民生,防止居民住房价格过快增长,计划出台合理的房价调控政策,为此有关部门抽样调查了100个楼盘的住房销售价格,右表是这100个楼盘住房销售均价(单位:千元/平米)的频率分布表,根据右表回答以下问题:
(1)求右表中a,b的值;
(2)请将下面的频率分布直方图补充完整,并根据直方图估计该市居民住房销售价格在4千元/平米到8千元/平米之间的概率.
| 分组 |
频数 |
频率 |
| [2,3) |
5 |
0.05 |
| [3,4) |
10 |
0.10 |
| [4,5) |
a |
0.15 |
| [5,6) |
24 |
0.24 |
| [6,7) |
18 |
0.18 |
| [7,8) |
12 |
b |
| [8,9) |
8 |
0.08 |
| [9,10) |
8 |
0.08 |
| 合计 |
100 |
1.00 |
设数列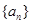 、
、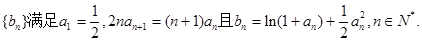
(1)求数列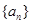 的通项公式;
的通项公式;
(2)对一切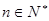 ,证明:
,证明: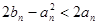 成立;
成立;
(3)记数列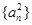 、
、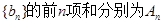 、
、
已知函数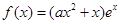 ,其中e是自然数的底数,
,其中e是自然数的底数,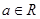 .
.
(1)当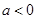 时,解不等式
时,解不等式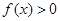 ;
;
(2)当 时,求整数k的所有值,使方程
时,求整数k的所有值,使方程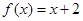 在[k,k+1]上有解;
在[k,k+1]上有解;
(3)若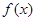 在[-1,1]上是单调增函数,求
在[-1,1]上是单调增函数,求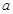 的取值范围.
的取值范围.
如图,椭圆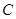 的中心在原点,焦点在
的中心在原点,焦点在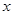 轴上,
轴上, 分别是椭圆
分别是椭圆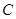 的左、右焦点,
的左、右焦点,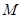 是椭圆短轴的一个端点,过
是椭圆短轴的一个端点,过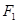 的直线
的直线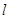 与椭圆交于
与椭圆交于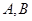 两点,
两点,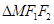 的面积为
的面积为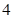 ,
,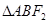 的周长为
的周长为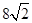 .
.
(1)求椭圆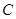 的方程;
的方程;
(2)设点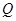 的坐标为
的坐标为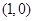 ,是否存在椭圆上的点
,是否存在椭圆上的点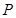 及以
及以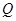 为圆心的一个圆,使得该圆与直线
为圆心的一个圆,使得该圆与直线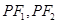 都相切,如存在,求出
都相切,如存在,求出 点坐标及圆的方程,如不存在,请说明理由.
点坐标及圆的方程,如不存在,请说明理由.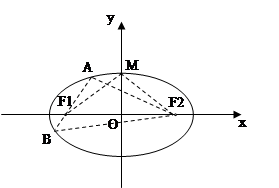
心理学家研究某位学生的学习情况发现:若这位学生刚学完的知识存留量记为1,则 天后
天后 的存留量
的存留量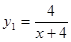 ;若在
;若在 天时进行第一次复习,则此时知识存留量比未复习情况下增加一倍(复习时间忽略不计),其后存储量
天时进行第一次复习,则此时知识存留量比未复习情况下增加一倍(复习时间忽略不计),其后存储量 随时间变化的曲线恰为直线的一部分,其斜率为
随时间变化的曲线恰为直线的一部分,其斜率为 存留量随时间变化的曲线如图所示.当进行第一次复习后的存留量与不复习的存留量相差最大时,则称此时此刻为“二次复习最佳时机点”.
存留量随时间变化的曲线如图所示.当进行第一次复习后的存留量与不复习的存留量相差最大时,则称此时此刻为“二次复习最佳时机点”.
(1)若 ,求“二次最佳时机点”;
,求“二次最佳时机点”;
(2)若出现了“二次复习最佳时机点”,求 的取值范围.
的取值范围.