已知函数f(x）="ax3" + x2 - ax (
且a
).
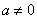(I) 若函数f(x)在{-∞，-1)和（
，+∞)上是增函数¥在（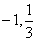
)上 是减函数，求a的值；
(II)讨论函数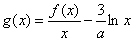
的单调递减区间；
(III)如果存在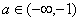
，使函数h(x)="f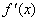(x)+" 
,x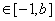
(b> - 1)，在x = -1处取得最小值，试求b的最大值.
已知函数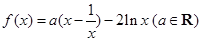
．
（1）若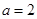
，求曲线
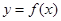在点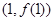
处的切线方程；
（2）求函数
的单调区间；
（3）设函数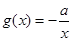
．若至少存在一个
，使得
成立，求实数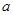
的取值范围．
已知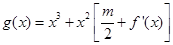
，
，
．
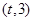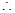（1）当
时，试比较
与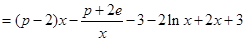
的大小关系；
（2）猜想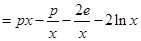
与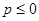
的大小关系，并给出证明．
已知在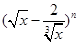
的展开式中，第5项的系数与第3项的系数之比是56：3．
（1）求展开式中的所有有理项；
（2）求展开式中系数绝对值最大的项．
（3）求
的值.
由数字1、2、3、4、5、6组成无重复数字的数中，求：
（1）六位偶数的个数；
（2）求三个偶数互不相邻的六位数的个数；
（3）求恰有两个偶数相邻的六位数的个数；
（4）奇数字从左到右，从小到大依次排列的六位数的个数．
已知复数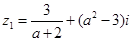
，
（
，
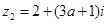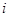是虚数单位）．
（1）若复数
在复平面上对应点落在第一象限，求实数
的取值范围；
（2）若虚数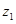
是实系数一元二次方程
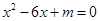的根，求实数
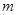值．