已知直线 ,
, .
. 为何值时,
为何值时, :(1)相交; (2)平行.
:(1)相交; (2)平行.
(本小题满分14分)
已知曲线 :
: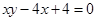 ,数列
,数列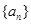 的首项
的首项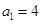 ,且当
,且当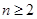 时,点
时,点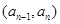 恒在曲线
恒在曲线 上,数列
上,数列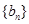 满足
满足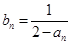 。
。
(1)试判断数列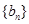 是否是等差数列?并说明理由;
是否是等差数列?并说明理由;
(2)求数列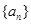 和
和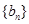 的通项公式;
的通项公式;
(3)设数列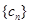 满足
满足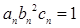 ,试比较数列
,试比较数列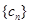 的前
的前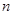 项和
项和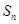 与2的大小。
与2的大小。
(本小题满分14分)
如图,沿等腰直角三角形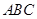 的中位线
的中位线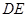 ,将平面
,将平面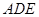 折起,平面
折起,平面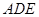 ⊥平面
⊥平面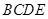 ,得到四棱锥
,得到四棱锥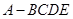 ,
,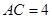 ,设
,设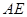 、
、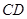 的中点分别为
的中点分别为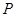 、
、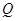 ,
,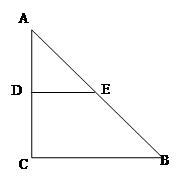
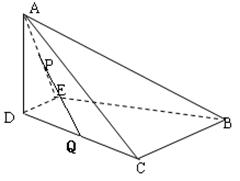
(1)求证:平面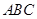 ⊥平面
⊥平面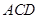
(2)求证:
(3)求平面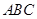 与平面
与平面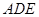 所成锐二面角的余弦值。
所成锐二面角的余弦值。
(本小题满分12分)
甲,乙两人进行乒乓球比赛,约定每局胜者得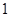 分,负者得
分,负者得 分,比赛进行到有一人比对方多
分,比赛进行到有一人比对方多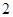 分或打满
分或打满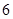 局时停止.设甲在每局中获胜的概率为
局时停止.设甲在每局中获胜的概率为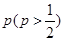 ,且各局胜负相互独立.若第二局比赛结束时比赛停止的概率为
,且各局胜负相互独立.若第二局比赛结束时比赛停止的概率为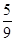 .
.
(1)求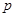 的值;
的值;
(2)设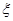 表示比赛停止时比赛的局数,求随机变量
表示比赛停止时比赛的局数,求随机变量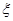 的分布列和数学期望
的分布列和数学期望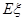 。
。
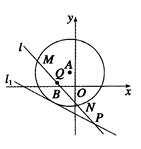
(本小题满分14分)如图所示,已知以点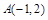 为圆心的圆与直线
为圆心的圆与直线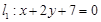 相切.过点
相切.过点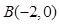 的动直线
的动直线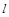 与圆
与圆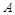 相交于
相交于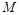 ,
, 两点,
两点,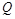 是
是 的中点,直线
的中点,直线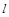 与
与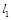 相交于点
相交于点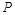 .
.
(1)求圆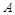 的方程;
的方程;
(2)当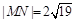 时,求直线
时,求直线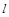 的方程.
的方程.
(3)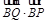 是否为定值?如果是,求出其定值;如果不是,请说明理由.
是否为定值?如果是,求出其定值;如果不是,请说明理由.
(本小题满分13分)已知以点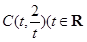
 为圆心的圆与
为圆心的圆与 轴交于点
轴交于点 、
、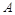 ,与
,与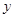 轴交于点
轴交于点 、
、 ,其中
,其中 为原点.
为原点.
(1)求证:△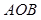 的面积为定值;
的面积为定值;
(2)设直线 与圆
与圆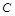 交于点
交于点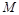 、
、 , 若
, 若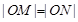 ,求圆
,求圆 的方程.
的方程.