如图, ⊙O为 的外接圆,直线
的外接圆,直线 为⊙O的切线,切点为
为⊙O的切线,切点为 ,直线
,直线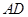 ∥
∥ ,交
,交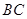 于
于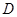 ,交⊙O于
,交⊙O于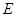 ,
, 为
为 上一点,且
上一点,且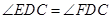 .
.
求证:(Ⅰ) ;
;
(Ⅱ)点 、
、 、
、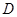 、
、 共圆.
共圆.
(本小题满分10分)
一位游客欲参观上海世博会中甲、乙、丙这3个展览馆,又该游客参观 甲、乙、丙这3个展览馆的概率分别是0.4,0.5,0.6,且是否参观哪个展览馆互不影响,设
甲、乙、丙这3个展览馆的概率分别是0.4,0.5,0.6,且是否参观哪个展览馆互不影响,设 表示该游客离开上海世博会时参观的展览馆数与没有参观的展览馆数之差的绝对值.
表示该游客离开上海世博会时参观的展览馆数与没有参观的展览馆数之差的绝对值.
(Ⅰ)求 的概率分布及数学期望;
的概率分布及数学期望;
(Ⅱ)记“函数 在区间
在区间
 上单调递增”为事件
上单调递增”为事件 ,求事件
,求事件 的概率.
的概率.
(本小题满分10分)
已知四棱锥P—ABCD的底面为直角梯形,AB//DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=1,AB=2,M是PB的中点。
(I)求AC与PB所 成角的余弦值;
成角的余弦值;
(II)求面AMC与面BMC所成二面角的余弦值的大小。
(选修4—5:不等式选讲)
设x是正数,求证:
(选修4—4:坐标系与参数方程)
已知两个圆的极坐标方程分别是 ,求这两个圆的圆心距。
,求这两个圆的圆心距。
(选修4—2:矩阵与变换)
已知矩阵 ,矩阵M对应的变换把曲线
,矩阵M对应的变换把曲线 变为曲线C,求曲线C的方程。
变为曲线C,求曲线C的方程。