已知,如图,在R t△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于D.

(1)以AB边上一点O为圆心,过A,D两点作⊙O(不写作法,保留作图痕迹),再判断直线BC与⊙O的位置关系,并说明理由;
(2)若(1)中的⊙O与AB边的另一个交点为E,半径为2,AB=6,求线段AD、AE与劣弧DE所围成的图形面积.(结果保留根号和 )
)
如图所示,以平行四边形ABCD的顶点A为圆心,AB为半径作圆,分别交BC,AD于E,F两点,交BA的延长于G,判断弧EF和弧FG是否相等,并说明理由。
如果三角形有一边上的中线恰好等于这边的长,那么称这个三角形为“有趣三角形”,这条中线称为“有趣中线”。如图,在三角形ABC中,∠C=90°,较短的一条直角边BC=1,且三角形ABC是“有趣三角形”,求三角形ABC的“有趣中线”的长。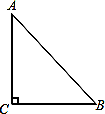
已知:如图,A、B、C为⊙O上的三个点,⊙O的直径为4cm,∠ACB=45°,求AB的长
已知二次函数y=x2+bx+c的图象过(2,-1)和(4,3)两点,求y=x2+bx+c的表达式
如图,已知∠1=∠2,∠AED=∠C,求证:△ABC∽△ADE