已知极坐标系的极点为直角坐标系 的原点,极轴为x轴的正半轴,两种坐标系中的长度单位相同,已知曲线
的原点,极轴为x轴的正半轴,两种坐标系中的长度单位相同,已知曲线 的极坐标方程为
的极坐标方程为 .
.
(1)求 的直角坐标方程;
的直角坐标方程;
(2)直线 (
( 为参数)与曲线C交于
为参数)与曲线C交于 ,
, 两点,与
两点,与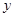 轴交于
轴交于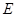 ,求
,求 的值.
的值.
(本小题满分14分)已知函数 (
( ).
).
(Ⅰ)当 时,求函数
时,求函数 的单调区间;
的单调区间;
(Ⅱ)当 时,
时, 取得极值.
取得极值.
(1)若 ,求函数
,求函数 在
在 上的最小值;
上的最小值;
(2)求证:对任意 ,都有
,都有 .
.
(本小题满分13分)如图,椭圆 :
: (
(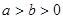 )和圆
)和圆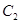 :
: ,已知圆
,已知圆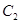 将椭圆
将椭圆 的长轴三等分,椭圆
的长轴三等分,椭圆 右焦点到直线
右焦点到直线 的距离为
的距离为 ,椭圆
,椭圆 的下顶点为
的下顶点为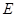 ,过坐标原点
,过坐标原点 且与坐标轴不重合的任意直线
且与坐标轴不重合的任意直线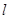 与圆
与圆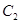 相交于点
相交于点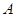 、
、 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)若直线 、
、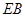 分别与椭圆
分别与椭圆 相交于另一个交点为点
相交于另一个交点为点 、
、 .
.
①求证:直线 经过一定点;
经过一定点;
|
②试问:是否存在以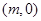 为圆心,
为圆心,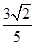 为半径的圆
为半径的圆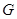 ,使得直线
,使得直线 和直线
和直线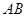 都与圆
都与圆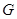 相交?若存在,请求出所有
相交?若存在,请求出所有 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(本小题满分12分)已知数列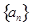 的前
的前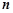 项和
项和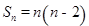 ,数列
,数列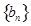 满足
满足 ,
,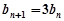 (
( ).
).
(Ⅰ)求数列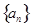 ,
,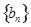 的通项公式;
的通项公式;
(Ⅱ)记数列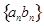 的前
的前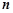 项和为
项和为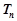 ,求
,求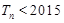 时的
时的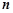 的最大值.
的最大值.
(本小题满分12分)2014年APEC峰会于11月10-11日在北京召开.据志愿服务联合会的统计显示:APEC领导人会议周期间,2000名志愿者共上岗服务11219人次,累计服务132022小时,所有的志愿者来自全国四大地理区域,数据如下表所示:
| 地理区域 |
北方地区 |
南方地区 |
西北地区 |
青藏地区 |
| 志愿者人数 |
600 |
800 |
400 |
200 |
为了更进一步了解有关信息,采用分层抽样的方法从上述四大地理区域的志愿者中随机抽取50名参加问卷调查.
(Ⅰ)从参加问卷调查的50名志愿者中随机抽取两名,求这两名来自同一地理区域的概率;
(Ⅱ)在参加问卷调查的50名志愿者中,从来自北方地区、西北地区的志愿者中随机抽取两名,用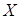 表示抽得北方地区志愿者的人数,求
表示抽得北方地区志愿者的人数,求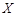 的分布列和数学期望.
的分布列和数学期望.
(本小题满分12分)在四棱锥P-ABCD中,底面ABCD是矩形,侧棱PA垂直于底面,E、F分别是AB、PC的中点. 
(Ⅰ)求证:EF∥平面PAD;
(Ⅱ)当平面PCD与平面ABCD成多大角时,直线EF⊥平面PCD?