已知圆O: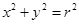 上的点到直线
上的点到直线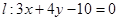 的最小距离为1,设P为直线
的最小距离为1,设P为直线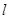 上的点,过P点作圆O的两条切线PA、PB, 其中A、B为切点.
上的点,过P点作圆O的两条切线PA、PB, 其中A、B为切点.
(1)求圆O的方程;
(2)当点P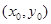 为直线
为直线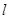 上的定点时,求直线AB的方程.
上的定点时,求直线AB的方程.
.(本小题满分10分)
已知 ,求证:
,求证: .
.
(本小题满分8分)
已知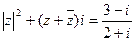 (i为虚数单位),求复数z.
(i为虚数单位),求复数z.
(本小题满分8分)
已知直线 的方程为
的方程为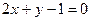 ,圆
,圆 的极坐标方程为
的极坐标方程为  .
.
(Ⅰ)将圆 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(Ⅱ)判断直线 和圆
和圆 的位置关系.
的位置关系.
若曲线C上的点到直线 的距离比它到点F
的距离比它到点F 的距离大1,
的距离大1,
(1)求曲线C的方程。
(2)过点F(1,0)作倾斜角为 的直线交曲线C于A、B两点,求AB的长
的直线交曲线C于A、B两点,求AB的长
(3)过点F(1,0)作斜率为k 的直线交曲线C于M、N 两点,求证: 为定值
为定值
温州某私营公司生产一种产品,根据历年的情况可知,生产该产品每天的固定成本为14000元,每生产一件该产品,成本增加210元.已知该产品的日销售量 与产量
与产量 之间的关系式为
之间的关系式为 ,每件产品的售价
,每件产品的售价 与产量
与产量 之间的关系式为
之间的关系式为 .
.
(Ⅰ)写出该公司的日销售利润 与产量
与产量 之间的关系式;
之间的关系式;
(Ⅱ)若要使得日销售利润最大,每天该生产多少件产品,并求出最大利润