甲、乙两个盒子中各有3个球,其中甲盒中有2个黑球1个白球,乙盒中有1个黑球2个白球,所有球之间只有颜色区别.
(Ⅰ)若从甲、乙两个盒子中各取一个球,求取出的2个球颜色相同的概率;
(Ⅱ)将这两个盒子中的球混合在一起,从中任取2个,求取出的2个球中至少有一个黑球的概率.
(本小题满分13分) 已知函数 (
( ).
).
(1)求函数 的单调区间;
的单调区间;
(2)函数 在定义域内是否存在零点?若存在,请指出有几个零点;若不存在,请说明理由;
在定义域内是否存在零点?若存在,请指出有几个零点;若不存在,请说明理由;
(3)若 ,当
,当 时,不等式
时,不等式 恒成立,求α的取值范围.
恒成立,求α的取值范围.
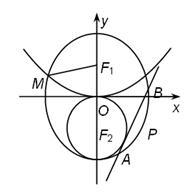
(本小题满分13分)已知 分另为椭圆的上、下焦点,
分另为椭圆的上、下焦点, 是抛物线
是抛物线 的焦点,点
的焦点,点 是
是 与
与 在第二象限的交点, 且
在第二象限的交点, 且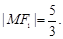
(1)求椭圆 的方程;
的方程;
(2)与圆 相切的直线
相切的直线 交椭圆
交椭圆 于
于 ,若椭圆
,若椭圆 上一点
上一点 满足
满足 ,求实数
,求实数 的取值范围.
的取值范围.
(本小题满分13分)设数列 的前
的前 项和为
项和为 ,对一切
,对一切 ,点
,点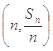 都在函数
都在函数 的图象上
的图象上
(1)求 归纳数列
归纳数列 的通项公式(不必证明);
的通项公式(不必证明);
(2)将数列 依次按1项、2项、3项、4项循环地分为(
依次按1项、2项、3项、4项循环地分为( ),
), ,
, ,
,  ;
; ,
, ,
, ,
, ;
; , ..,
, ..,
分别计算各个括号内各数之和,设由这些和按原来括号的前后顺序构成的数列为 ,求
,求 的值;
的值;
(3)设 为数列
为数列 的前
的前 项积,若不等式
项积,若不等式 对一切
对一切  都成立,其中
都成立,其中 ,求
,求 的取值范围
的取值范围
(本小题满分12分)如图,在四棱锥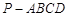 中,
中, 平面
平面 ,
, ,且
,且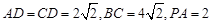 ,点
,点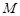 在
在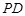 上.
上.
(1)求证: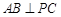 ;
;
(2)若二面角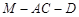 的大小为
的大小为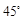 ,求
,求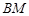 与平面
与平面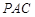 所成角的正弦值.
所成角的正弦值.
(本小题满分12分)在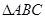 中,角
中,角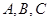 所对的边分别为
所对的边分别为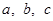 ,满足
,满足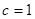 ,且
,且 .
.
(1)求C的大小;
(2)求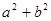 的最大值,并求取得最大值时角A,B的值.
的最大值,并求取得最大值时角A,B的值.