设全集U=R,A={y|y= },B={x|y=ln(1-2x)}.
},B={x|y=ln(1-2x)}.
(1)求A∩(CUB);
(2)记命题p:x∈A,命题q:x∈B,求满足“p∧q”为假的x的取值范围.
(本小题满分12分)如图,在四棱锥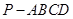 中,底面
中,底面 是
是 且边长为
且边长为 的菱形,侧面
的菱形,侧面 是等边三角形,且平面
是等边三角形,且平面 ⊥底面
⊥底面 ,
, 为
为 的中点.
的中点.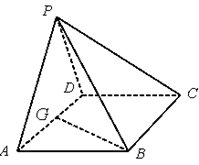
(1)求证:
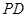 ;
;
(2)求点 到平面
到平面 的距离.
的距离.
(本小题满分12分)已知等差数列 的前
的前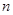 项和
项和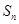 满足
满足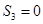 ,
,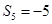 .
.
(1)求 的通项公式;
的通项公式;
(2)求数列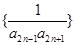 的前
的前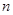 项和.
项和.
(本小题满分10分)选修4-5:不等式选讲.
已知函数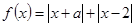 .
.
(1)当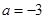 时,求不等式
时,求不等式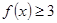 的解集;
的解集;
(2)若 的解集包含
的解集包含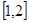 ,求
,求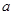 的取值范围.
的取值范围.
(本小题满分10分)选修4—4:坐标系与参数方程选讲.
已知直线经过点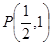 ,倾斜角
,倾斜角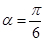 ,圆C的极坐标方程为
,圆C的极坐标方程为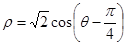
(1)写出直线的参数方程,并把圆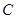 的方程化为直角坐标方程;
的方程化为直角坐标方程;
(2)设与圆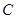 相交于两点
相交于两点 ,求点
,求点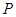 到
到 两点的距离之积.
两点的距离之积.
(本小题满分10分)选修4—1:几何证明选讲.
如图,AB是圆O的直径,C是半径OB的中点,D是OB延长线上一点,且BD=OB,直线MD与圆O
交于点M、T(不与A、B重合),DN与圆O相切于点N,连结MC,MB,OT.
(1)求证: ;
;
(2)若 ,试求
,试求 的大小.
的大小.