【改编】(本小题满分14分)已知数列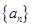 的前
的前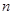 项和是
项和是 ,且
,且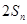 ,
,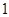 ,
, 成等差数列.
成等差数列.
(1)求数列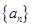 的通项公式;
的通项公式;
(2)设 (
( ),求适合方程
),求适合方程 的正整数
的正整数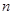 的值.
的值.
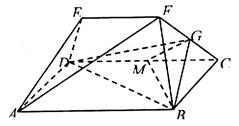
(本小题满分14分)如图几何体中,四边形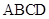 为矩形,
为矩形,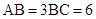 ,
,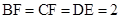 ,
,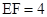 ,
,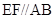 ,
, 为
为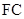 的中点,
的中点,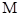 为线段
为线段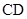 上的一点,且
上的一点,且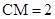 .
.
(1)证明: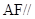 平面
平面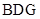 ;
;
(2)证明:平面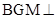 平面
平面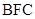 ;
;
(3)求三棱锥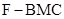 的体积
的体积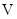 .
.
(本小题满分12分)某次的一次学科测试成绩的茎叶图和频率分布直方图都受到不同程度的
污损,可见部分如图.
(1)求参加测试的总人数及分数在 之间的人数;
之间的人数;
(2)若要从分数在 之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,恰有一份分
之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,恰有一份分
数在 之间的概率.
之间的概率.
【原创】(本小题满分12分)已知向量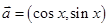 ,
,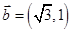 ,设函数
,设函数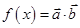 .
.
(1)求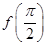 的值;
的值;
(2)若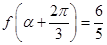 ,
,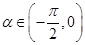 ,求
,求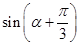 的值.
的值.
(本小题满分14分)已知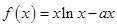 ,
,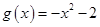 .
.
(1)当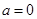 时,求函数
时,求函数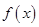 的单调区间;
的单调区间;
(2)对一切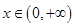 ,
,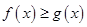 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.