为了了解初三学生女生身高情况,某中学对初三女生身高进行了一次测量,所得数据整理后列出了频率分布表如下:
| 组 别 |
频数 |
频率 |
| [145.5,149.5) |
1 |
0.02 |
| [149.5,153.5) |
4 |
0.08 |
| [153.5,157.5) |
20 |
0.40 |
| [157.5,161.5) |
15 |
0.30 |
| [161.5,165.5) |
8 |
0.16 |
| [165.5,169.5) |
m |
n |
| 合 计 |
M |
N |
(1)求出表中 所表示的数;
所表示的数;
(2)画出频率分布直方图;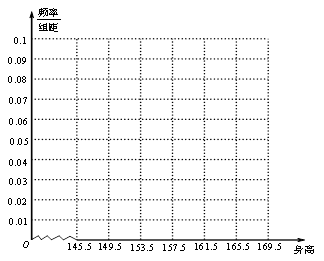
在△ABC中, 分别为角A、B、C的对边,
分别为角A、B、C的对边,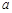 =3,△ABC的面积为6,
=3,△ABC的面积为6, ,D为△ABC内任一点,点D到三边距离之和为
,D为△ABC内任一点,点D到三边距离之和为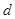 。
。
(1)求:角A的正弦值;
(2)求:边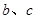 ;
;
(3)求: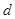 的取值范围
的取值范围
已知正项等差数列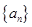 的前
的前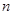 项和为
项和为 ,若
,若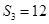 ,且
,且 成等比数列.
成等比数列.
(Ⅰ)求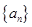 的通项公式;
的通项公式;
(Ⅱ)记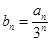 的前
的前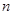 项和为
项和为 ,求
,求 .
.
如图,设 是单位圆和
是单位圆和 轴正半轴的交点,
轴正半轴的交点, 是单位圆上的两点,
是单位圆上的两点, 是坐标原点,
是坐标原点, ,
, .
.
(1)若 ,求
,求 的值;
的值;
(2)设函数 ,求
,求 的值域.
的值域.
在等比数列{ }中,
}中, ,公比
,公比 ,且
,且 ,
,  与
与 的等比中项为2.
的等比中项为2.
(1)求数列{ }的通项公式;
}的通项公式;
(2)设 ,求:数列{
,求:数列{ }的前
}的前 项和为
项和为 ,
,
设函数 ,
, .
.
(1)当 时,函数
时,函数 取得极值,求
取得极值,求 的值;
的值;
(2)当 时,求函数
时,求函数 在区间[1,2]上的最大值;
在区间[1,2]上的最大值;
(3)当 时,关于
时,关于 的方程
的方程
 有唯一实数解,求实数
有唯一实数解,求实数 的值.
的值.