甲、乙两公司参与一项治理大气净化工程,如果两公司合做,12天可以完成;如果两公司单独完成此项公程,乙公司所用时间是甲公司的1.5倍。
(1)甲、乙公司单独完成此项工程,各需多少天?
(2)已知这项工程甲、乙两公司合做共需付施工费102 000元,乙公司每天的施工费比甲公司每天的施工费少1500元. 若让一个公司单独完成这项工程,哪个公司施工费较少?
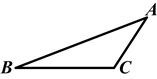
如图,这是某城市古建筑群中一座古塔底部的建筑平面图,请你利用学过的知识设计如何测量出古塔外墙底部的∠ABC大小的方案,并说明理由.
按图的方法折纸,然后回答问题: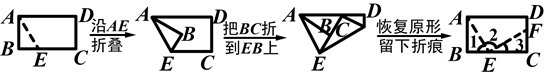
(1)∠2是多少度?为什么?
(2)∠1与∠3有何关系?
(3)∠1与∠AEC,∠3与∠BEF分别有何关系?
如图①,∠AOB,∠COD都是直角.
(1)试猜想∠AOD和∠BOC在数量上是否存在相等、互余或互补关系,你能说明你猜想的正确性吗?
(2)当∠COD绕点O旋转到如图②的位置时,你的猜想还成立吗?为什么?
如图,直线DE和BC被直线AB所截.
(1)∠1与∠2,∠1与∠3,∠1与∠4各是什么角?
(2)∠1与∠5是内错角吗?
(3)如果∠1+∠3=180°,那么∠1等于∠2吗?∠1和∠5互补吗?为什么?
如图所示,过点A作BC的垂线.