（本小题满分10分）
如图（1），在平面直角坐标系中，△OAB三个顶点坐标分别为O（0，0），A（1，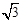
），B（4，0）．
（1）求证：AB⊥OA
（2）在第一象限内确定点M，使△MOB与△AOB相似，求符合条件的点M的坐标．
（3）如图（2），已知D（0，-3），作直线BD．
①将△AOB沿射线BD平移4个单位长度后，求△AOB与以D为圆心，以1为半径的⊙D的公共点的个数．
②如图（3），现有一点P从D点出发，沿射线DB的方向以1个单位长度/秒的速度作匀速运动，运动时间为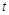
秒．当以P为圆心，以
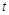为半径的⊙P与△AOB有公共点时，求的取值范围．
如图，我县某校新建了一座陶铸雕塑，小林站在距离雕塑2.7米的A处自B点看雕塑头顶D的仰角为45°，看雕塑底部C的仰角为30°，求塑像CD的高度．（最后结果精确到0.1米，参考数据：
）
先化简，再求值：（a2b+ab）÷
，其中a=
，b=
．
（1）计算：24﹣
+|1﹣4sin60°|+（π﹣
）0；
（2）解方程：
．
如图，在平面直角坐标系中，直线AB与x轴、y轴分别交于点A、B，直线CD与x轴、y轴分别交于点C、D，AB与CD相交于点E，线段OA、OC的长是一元二次方程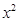
－18x+72=0的两根（OA＞OC），BE=5，tan∠ABO=
．
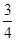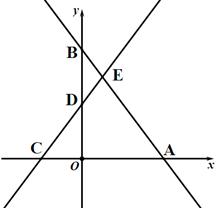
（1）求点A，C的坐标；
（2）若反比例函数y=
的图象经过点E，求k的值；
（3）若点P在坐标轴上，在平面内是否存在一点Q，使以点C，E，P，Q为顶点的四边形是矩形？若存在，请写出满足条件的点Q的个数，并直接写出位于x轴下方的点Q的坐标；若不存在，请说明理由．
某工厂计划生产A、B两种产品共60件，需购买甲、乙两种材料.生产一件A产品需甲种材料4千克，乙种材料1千克；生产一件B产品需甲、乙两种材料各3千克.经测算，购买甲、乙两种材料各1千克共需资金60元；购买甲种材料2千克和乙种材料3千克共需资金155元.
（1）甲、乙两种材料每千克分别是多少元？
（2）现工厂用于购买甲、乙两种材料的资金不能超过10000元，且生产B产品要超过38件，问有哪几种符合条件的生产方案？
（3）在（2）的条件下，若生产一件A产品需加工费40元，若生产一件B产品需加工费50元，应选择哪种生产方案，才能使生产这批产品的成本最低？请直接写出方案。