某工厂计划生产A、B两种产品共60件，需购买甲、乙两种材料.生产一件A产品需甲种材料4千克，乙种材料1千克；生产一件B产品需甲、乙两种材料各3千克.经测算，购买甲、乙两种材料各1千克共需资金60元；购买甲种材料2千克和乙种材料3千克共需资金155元.
（1）甲、乙两种材料每千克分别是多少元？
（2）现工厂用于购买甲、乙两种材料的资金不能超过10000元，且生产B产品要超过38件，问有哪几种符合条件的生产方案？
（3）在（2）的条件下，若生产一件A产品需加工费40元，若生产一件B产品需加工费50元，应选择哪种生产方案，才能使生产这批产品的成本最低？请直接写出方案。
如图，一次函数
与反比例函数
的图象交于点
和
，与y轴交于点C.
（1）
=，
=；
（2）根据函数图象可知，当
＞
时，x的取值范围是；
（3）过点A作AD⊥x轴于点D，点P是反比例函数在第一象限的图象上一点.设直线OP与线段AD交于点E，当
：
=3：1时，求点P的坐标.
(9分)如图所示，中原福塔(河南广播电视塔)是世界第—高钢塔．小明所在的课外活动小组在距地面268米高的室外观光层的点D处，测得地面上点B的俯角α为45°，点D到AO的距离DG为10米；从地面上的点B沿BO方向走50米到达点C处，测得塔尖A的仰角β为60°。请你根据以上数据计算塔高AO，并求出计算结果与实际塔高388米之间的误差．(参考数据：
≈1.732，
≈1.414.结果精确到0.1米)
.(9分)为更好地宣传“开车不喝酒，喝酒不开车”的驾车理念，某市一家报社设计了如右的调查问卷(单选).
在随机调查了奉市全部5 000名司机中的部分司机后，统计整理并制作了如下的统计图：
根据以上信息解答下列问题：
(1)补全条形统计图，并计算扇形统计图中m=；
(2)该市支持选项B的司机大约有多少人？
(3)若要从该市支持选项B的司机中随机选择100名，给他们发放“请勿酒驾”的提醒标志，则支持该选项的司机小李被选中的概率是多少?
如图，在梯形ABCD中，AD∥BC，延长CB到点E，使BE=AD，连接DE交AB于点M.
（1）求证：△AMD≌△BME；
（2）若N是CD的中点，且MN
=5，BE=2，求BC的长.
先化简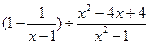
，然后从－2≤x≤2的范围内选取一个合适的整数作为x的值代入求值.