如图,点E是DF上一点,点B在AC上,∠1=∠2,∠C=∠D,试说明DF∥AC的理由。
理由:∵∠1=∠2 (已知)
∠1=∠3,∠2=∠4 ( )
∴∠3=∠4 ( )
∴______∥______ ( )
∴∠C=∠DBA ( )
又∵∠C=∠D ( 已知 )
∴∠DBA=∠D ( )
∴DF∥AC ( )
如图,长方体的底面是边长为1cm 的正方形,高为3cm.
(1)如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B,请计算所用细线最短需要cm?
(2)如果从点A开始经过4个侧面缠绕3圈到达点B,那么所用细线最短需要 cm.(直接填空)
如图,点B、F、C、E在一条直线上,BF=EC,AB∥ED,AC∥FD,求证:AC=DF.
如图:在8 8的正方形网格中,已知网格中小正方形的边长为1,
8的正方形网格中,已知网格中小正方形的边长为1, 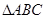 的三个顶点在格点上。
的三个顶点在格点上。
(1)画出 关于直线
关于直线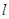 的对称图形
的对称图形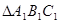 ;
;
(2)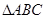 _____________直角三角形(填“是”或“不是”
_____________直角三角形(填“是”或“不是”
(3)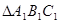 的面积是_____________
的面积是_____________
尺规作图:某学校正在进行校园环境的改造工程设计,准备在校内一块四边形花坛内栽上一棵桂花树.如图,要求桂花树的位置(视为点P),到花坛的两边AB、BC的距离相等,并且点P到点A、D的距离也相等.请用尺规作图作出栽种桂花树的位置点P(不写作法,保留作图痕迹).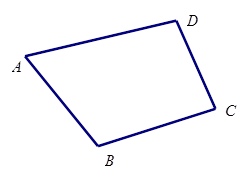
如图,已知正方形ABCD的边长为10cm,点E在边AB上,且AE=4cm,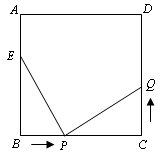
(1)如果点P在线段BC上以2cm/s的速度由B点向C点运动,同时,点Q在线段CD上由C点向D点运动.
①若点Q的运动速度与点P的运动速度相等,经过2秒后,△BPE与△CQP是否全等?请说明理由.
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为________cm/s时,在某一时刻也能够使△BPE与△CQP全等.
(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿正方形ABCD的四条边运动.求经过多少秒后,点P与点Q第一次相遇,并写出第一次相遇点在何处?