如图，已知正方形ABCD的边长为10cm，点E在边AB上，且AE=4cm，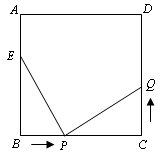
（1）如果点P在线段BC上以2cm／s的速度由B点向C点运动，同时，点Q在线段CD上由C点向D点运动．
①若点Q的运动速度与点P的运动速度相等，经过2秒后，△BPE与△CQP是否全等?请说明理由.
②若点Q的运动速度与点P的运动速度不相等，当点Q的运动速度为________cm/s时，在某一时刻也能够使△BPE与△CQP全等．
（2）若点Q以②中的运动速度从点C出发，点P以原来的运动速度从点B同时出发，都逆时针沿正方形ABCD的四条边运动．求经过多少秒后，点P与点Q第一次相遇，并写出第一次相遇点在何处？
今年，号称“千湖之省”的湖北正遭受大旱，为提高学生环保意识，节约用水，某校数学教师编造了一道应用题：
| 月用水量（吨） |
单价（元/吨） |
| 不大于10吨部分 |
1.5 |
| 大于10吨不大于m吨部分（20≤m≤50） |
2 |
| 大于m吨部分 |
3 |
为了保护水资源，某市制定一套节水的管理措施，其中对居民生活用水收费作如下规定：
（1）若某用户六月份用水量为18吨，求其应缴纳的水费；
（2）记该户六月份用水量为x吨，缴纳水费y元，试列出y关于x的函数式；
（3）若该用户六月份用水量为40吨，缴纳消费y元的取值范围为70≤y≤90，试求m的取值范围。
为庆祝建党90周年，某学校欲按如下规则组建一个学生合唱团参加我市的唱红歌比赛。
规则一：合唱团的总人数不得少于50人，且不得超过55人。
规则二：合唱团的队员中，九年级学生占合唱团总人数的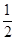
，八年级学生占合唱团总人数
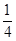，余下的为七年级学生。
请求出该合唱团中七年级学生的人数。
2011年5月20日是第22个中国学生营养日，某校社会实践小组在这天开展活动，调查快餐营养情况．他们从食品安全监督部门获取了一份快餐的信息（如图）．根据信息，解答下列问题．
(1)求这份快餐中所含脂肪质量；
(2)若碳水化合物占快餐总质量的40%，求这份快餐所含蛋白质的质量；
(3)若这份快餐中蛋白质和碳水化合物所占百分比的和不高于85%，求其中所含碳水化合物质量的最大值．
(2011浙江绍兴，22，12分)筹建中的城南中学需720套担任课桌椅（如图），光明厂承担了这项生产任务，该厂生产桌子的必须5人一组，每组每天可生产12张；生产椅子的必须4人一组，每组每天可生产24把.已知学校筹建组要求光明厂6天完成这项生产任务.
（1）问光明厂平均每天要生产多少套单人课桌椅？
（2）先学校筹建组组要求至少提前1天完成这项生产任务，光明厂生产课桌椅的员工增加到84名，试给出一种分配生产桌子、椅子的员工数的方案.
某小区前坪有一块空地，现想建成一块面积大于48平方米，周长小于34米的矩形绿化草地，已知一边长为8米，设其邻边长为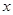
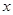米，求的整数解.
