如图，防洪大堤的横断面是梯形，背水坡AB的坡度i=1：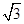
，且AB=20m．身高为1.7m的小明站在大堤A点，测得髙压电线杆顶端点D的仰角为30°．已知地面CB宽30m，求小明到电线杆的距离和髙压电线杆CD的髙度（结果保留根号）.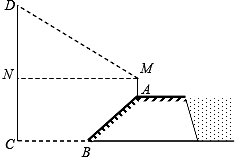
在直角坐标平面内，二次函数图象的顶点为A（1，﹣4），且过点B（3，0）．
（1）求该二次函数的解析式；
（2）将该二次函数图象向右平移几个单位，可使平移后所得图象经过坐标原点？并直接写出平移后所得图象与x轴的另一个交点的坐标．
如图，PA为⊙O的切线，A为切点，⊙O的割线PBC过点O与⊙O分别交于B、C，PA=8cm，PB=4cm，求⊙O的半径．
如图，正方形ABCD中，E与F分别是AD、BC上一点，在①AE=CF、②BE∥DF、③∠1=∠2中，请选择其中一个条件，证明BE=DF．
若关于x的一元二次方程x2+4x+2k=0有两个实数根，求k的取值范围及k的非负整数值．
解方程：（1）x2+4x+1="0" （2）（x﹣1）2+2x（x﹣1）=0．