如图所示,小球沿光滑的水平面冲上一个光滑的半圆形轨道,已知轨道的半径为R,小球到达轨道的最高点时对轨道的压力大小恰好等于小球的重力。请求出:
(1)小球到达轨道最高点时的速度为多大;
(2)小球落地时距离A点多远;落地时速度多大?
如图所示,摆长为L的单摆,当摆球由A经平衡位置O向右运动的瞬间,另一小球B以速度v同时通过平衡位置向右运动,B与水平面无摩擦,与竖直墙壁碰撞无能量损失,问OC间距离x满足什么条件,才能使B返回时与A球相遇?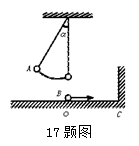
如图所示,细绳一端系着质量M=0.6 kg的物体,静止于水平面上,另一端通过光滑小孔吊着质量m=0.3 kg的物体,M的中点与圆孔距离为0.2 m,并知M和水平面的最大静摩擦力为2 N.现使此平面绕中心轴线转动,问角速度ω在什么范围m会处于静止状态?(g取10 m/s2)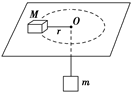
2011年9月29日21时16分天宫一号顺利发射升空,这是中国向空间站时代迈出的坚实一步。天宫一号经过两次变轨,进入高度约343千米的圆形对接轨道,此时的运动可以视作匀速圆周运动。等待11月份与神八交会对接。若地球半径为6400km。地球表面重力加速度g=10m/s2.
(1)则天宫一号的运行速度多大?
(2)则天宫一号的运行周期约为多少分钟?
有一根长为2L的轻质细线,它的两端固定在一根长为L的竖直转轴AB上,线上套一个可以自由移动的质量为m的小球.当转轴转动时,小球正好以B为圆心,在水平面内做匀速圆周运动.求细线的张力和小球的线速度.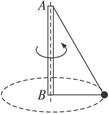
摩托车障碍赛中,运动员在水平路面上遇到一个壕沟,壕沟的尺寸如图6所示,要安全的越过这壕沟,求摩托车的速度v0至少为多大?(空气阻力不计, g=10m/s2)