如图所示,摆长为L的单摆,当摆球由A经平衡位置O向右运动的瞬间,另一小球B以速度v同时通过平衡位置向右运动,B与水平面无摩擦,与竖直墙壁碰撞无能量损失,问OC间距离x满足什么条件,才能使B返回时与A球相遇?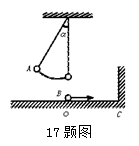
精确的研究表明,不同的原子核,其核子的平均质量(原子核的质量除以核子数)与原子序数有如图9所示的关系。
(1)试根据此图说出至少两条相关信息。
(2)太阳的能量来自下面的反应:四个质子(氢核)聚变成一个α粒子,同时发射两个正电子和两个没有静止质量的中微子,已知氢气燃烧与氧气化合生成水,每形成一个水分子释放的能量为6.2 eV,若想产生相当于太阳上1 kg的氢核聚变成α粒子所释放的能量,须燃烧多少千克氢气?α粒子质量mα="4.0026" u,质子质量mp="1.00783" u,电子质量me=5.48×10-4 u(u为原子质量单位,1u=1.6606×10-27kg,1u相当于931.5MeV的能量)
如图8所示,在测玻璃砖的折射率的实验中,多次改变入射角,测得入射角i及入射点和出射点处法线间距a,将数据在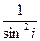 ~
~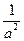 坐标系中绘制出相应图像,通过图像,写出计算玻璃砖折射率n的表达方式(答题时不一定作图)。
坐标系中绘制出相应图像,通过图像,写出计算玻璃砖折射率n的表达方式(答题时不一定作图)。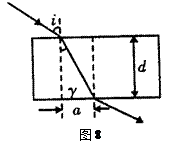
F1是英文Formula One的缩写,即一级方程式赛车,是仅次于奥运会和世界杯的世界第三大赛事。F1 赛车的变速系统非常强劲,从时速0加速到100 km/h仅需2.3秒,此时加速度仍达10m/s2,时速为200 km/h时的加速度仍有3m/s2,从0加速到200 km/h再急停到0只需12秒。假定F1 赛车加速时的加速度随时间的增大而均匀减小,急停时的加速度大小恒为9.2 m/s2。上海F1赛道全长5.451km,比赛要求选手跑完56圈决出胜负。求:
(1)若某车手平均时速为210km/h,则跑完全程用时为多少时分秒?
(2)该车手的F1 赛车的最大加速度。
(10分) 红宝石激光器发射的激光是不连续的一道道的闪光,每道闪光称为一个光脉冲。现有一红宝石激光器,发射功率为P=1.0×106W,所发射的光脉冲持续时间△t=1.0×10—11s,波长为693.4nm(1nm=10—9m),求:
(1)每个光脉冲的长度;
(2)每个光脉冲含有的光子数。(h=6.63×10—34J·s)
某电视台娱乐节目在游乐园举行家庭搬运砖块比赛活动,比赛规则是:向滑动行驶的小车上搬放砖块,且每次只能将一块砖无初速(相对地面)地放到车上,车停止时立即停止搬放,以车上砖块多少决定胜负。已知每块砖的质量m=0.8kg,小车的上表面光滑且足够长,比赛过程中车始终受到恒定的牵引力F=20N的作用,未放砖块时车以v0=3m/s的速度匀速前进。获得冠军的家庭上场比赛时每隔T=0.8s搬放一块砖,从放上第一块砖开始计时,图中仅画出了0~0.8s内车运动的v-t图象,g取10m/s2。求:
(1)小车的质量及车与地面间的动摩擦因数。
(2)车停止时,车上放有多少块砖。
