如图所示，两根竖直固定的足够长的金属导轨ad和bc相距L=0.2m，另外两根水平金属杆MN和EF的质量均为m=10-2kg，可沿导轨无摩擦地滑动，MN杆和EF杆的电阻均为0.2Ω（竖直金属导轨的电阻不计），EF杆放置在水平绝缘平台上，整个装置处于匀强磁场内，磁场方向垂直于导轨平面向里，磁感应强B=1.0T，现让MN杆在恒定拉力作用下由静止开始向上加速运动，当MN杆向上运动了0.5m后速度达到最大，此时EF杆恰好对绝缘平台的压力为零。（g取10m/s2）
试求：
（1）达到最大速度时 ，拉力对MN杆做功的功率；
（2）这一过程中，MNEF回路中产生的焦耳热。
如图所示，轻质弹簧的劲度系数k＝20 N/cm，用其拉着一个重为200 N的物体在水平面上运动，当弹簧的伸长量为4 cm时，物体恰在水平面上做匀速直线运动，求：
(1)物体与水平面间的动摩擦因数．
(2)当弹簧的伸长量为6 cm时，物体受到的水平拉力多大？这时物体受到的摩擦力有多大？
(3)如果物体在运动的过程中突然撤去弹簧，而物体在水平面上能继续滑行，这时物体受到的摩擦力多大？
带负电的小物体A放在倾角为θ（sinθ＝0.6）的绝缘斜面上，整个斜面处于范围足够大、方向水平向右的匀强电场中，如图所示。物体A的质量为m、电量为－q，与斜面间的动摩擦因数为μ，它在电场中受到的电场力的大小等于重力的一半。物体A在斜面上由静止开始下滑，经时间t后突然在斜面区域加上范围足够大的匀强磁场，磁场方向与电场强度方向垂直，磁感应强度大小为B，此后物体A沿斜面继续下滑距离L后离开斜面。重力加速度为g。求：
（1）物体A在斜面上的运动情况？说明理由。
（2）加磁场前A沿斜面运动的距离为多少？
（3）物体A在斜面上运动过程中有多少能量转化为内能？（结果用字母表示）
有一质量为m的卫星以轨道半径为r、周期为T环绕某行星做圆轨道运动，已知引力常量为G。求：
（1）行星的质量M；
（2）作用于卫星上的引力F；
（3）若行星的半径是卫星轨道半径的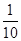
，行星表面的重力加速度g是多大？
如图所示，竖直悬挂的弹簧测力计吊一物体，处于静止状态，弹簧测力计示数表示物体对弹簧的拉力，其大小为F，试论证物体受到重力大小等于F，每一步推导都要写出所根据的物理规律。
如图所示，一带电粒子以某一速度在竖直平面内做直线运动，经过一段时间后进入一垂直于纸面向里、磁感应强度为B的最小的圆形匀强磁场区域（图中未画出磁场区域），粒子飞出磁场后垂直电场方向进入宽为L的匀强电场。电场强度大小为E，方向竖直向上。当粒子穿出电场时速度大小变为原来的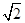
倍。已知带电粒子的质量为m，电量为g，重力不计。粒子进入磁场前的速度如图与水平方向成θ＝60°角。求：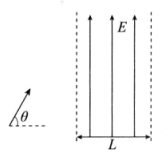
（1）粒子带什么性质的电荷；
（2）粒子在磁场中运动时速度多大；
（3）该最小的圆形磁场区域的面积为多大？