在三棱柱ABC-A1B1C1中,侧面ABB1A1为矩形,AB=1,AA1= ,D为AA1中点,BD与AB1交于点O,CO丄侧面ABB1A1.
,D为AA1中点,BD与AB1交于点O,CO丄侧面ABB1A1.
(Ⅰ)证明:BC丄AB1;
(Ⅱ)若OC=OA,求二面角C1-BD-C的余弦值.
如图,四边形 为矩形,
为矩形, 平面
平面 ,
, ,
, 平面
平面 于点
于点 ,且点
,且点 在
在 上.
上.
(1)求证: ;
;
(2)求四棱锥 的体积;
的体积;
(3)设点 在线段
在线段 上,且
上,且 ,试在线段
,试在线段 上确定一点
上确定一点 ,使得
,使得 平面
平面 .
.
已知函数 ,
, .
.
(1)求函数 的最小正周期;
的最小正周期;
(2)求函数 在区间
在区间 上的最大值和最小值.
上的最大值和最小值.
已知全体实数集 ,集合
,集合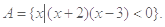

(1)若 时,求
时,求 ;
;
(2)设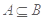 ,求实数
,求实数 的取值范围.
的取值范围.
已知函数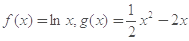 .
.
(1)设 (其中
(其中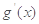 是
是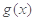 的导函数),求
的导函数),求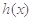 的最大值;
的最大值;
(2)求证: 当 时,有
时,有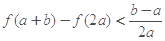 ;
;
(3)设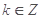 ,当
,当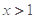 时,不等式
时,不等式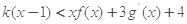 恒成立,求
恒成立,求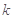 的最大值.
的最大值.
已知三点O(0,0),A(-2,1),B(2,1),曲线C上任意一点M(x,y)满足| +
+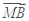 |=
|=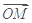 ·(
·(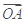 +
+ )+2.
)+2.
(1)求曲线C的方程;
(2)点Q(x0,y0)(-2<x0<2)是曲线C上的动点,曲线C在点Q处的切线为 ,点P的坐标是(0,-1),
,点P的坐标是(0,-1), 与PA,PB分别交于点D,E,求△QAB与△PDE的面积之比.
与PA,PB分别交于点D,E,求△QAB与△PDE的面积之比.