如图所示,水平放置的圆盘半径为R=1m,在其边缘C点固定一个高度不计的小桶,在圆盘直径CD的正上方放置一条水平滑道AB,滑道与CD平行.滑道右端B与圆盘圆心O在同一竖直线上,其高度差为h=1.25m.在滑道左端静止放置质量为m=0.4kg的物块(可视为质点),物体与滑道间的动摩擦因数为μ=0.2.当用一大小为F=4N的水平向右拉力拉动物块的同时,圆盘从图示位置以角速度ω=2πrad/s,绕穿过圆心O的竖直轴匀速转动,拉力作用一段时间后撤掉,物块在滑道上继续滑行,由B点水平抛出,恰好落入小桶内,重力加速度取10m/s2.
(1)求拉力作用的最短时间;
(2)若拉力作用时间为0.5s,求所需滑道的长度.
猎狗能以最大速度v1=10m/s持续地奔跑,野兔只能以最大速度v2=8m/s的速度持续奔跑。一只野兔在离洞窟s1=200m处的草地上玩耍,猎狗发现野兔后径直朝野兔追来。兔子发现猎狗时,与猎狗相距s2=60m且猎狗速度已达最大,兔子立即掉头跑向洞窟。设猎狗、野兔、洞窟总在同一直线上,求:野兔必须在多少时间内回到洞窟才能保证安全;
野兔的加速度至少要多大才能保证安全回到洞窟。
某兴趣小组做了一个电场中的过山车小实验。如图所示的绝缘轨道ABCDF处在竖直向下的匀强电场中,其中倾斜轨道AB和竖直的圆形轨道光滑,水平轨道BCF粗糙,C为圆形轨道的最低点,BC段长为L。现有一个质量为m、带电量为-q的小球,从距水平面BC高h=5.4L处的P点由静止下滑,小球恰能通过竖直圆形轨道的最高点D而作圆周运动。已知小球与水平轨道BCF间的动摩擦因素为μ=0.4,空间所加的电场强度为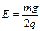 。请问:
。请问: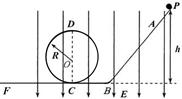
圆形轨道半径R的大小为多少?
为使小球不滑出CF,那么水平轨道CF的长度至少为多少?
现改变h高度,为使小球最终停在B点,请问小球释放点高度h要满足什么要求
 ?
?
环保汽车已越来越走进我们的生活,某辆以蓄电池为驱动能源的环保汽车,总质量m=3×103 kg。当它在水平路面上以v=36 km/h的速度匀速行驶时,驱动电机的输入电流I=50 A,电压U=30 0 V。在此行驶状态下:
0 V。在此行驶状态下:求驱动电机的输入功率P电;
若驱动电机能够将输入功率的90%转化为用于牵引汽车前进的机械功率P机,求汽车所受阻力与车重的比值(g取10 m/s2);
设想改用太阳能电池给该车供电,其他条件不变,求所需的太阳能电池板的最小面积。
已知太阳辐射的总功率P0=4×1026 W,太阳到地球的距离r=1.5×1011 m,太阳光传播到达地面的过程中大约有30%的能量损耗,该车所用太阳能电池的能量转化效率约为15%。已知球面面积计算公式为 。
。
如图所示,有一电子(电荷量为e)经电压U0加速后,进入两块间距为d、电压为U的平行金属板间.若电子从两板正中间垂直电场方向射入,且正好能穿过电场,求: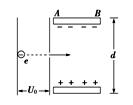
金属板AB的长度;
电子穿出电场时的动能.
如图所示,在场强为E的匀强电场中,一电子(电量为e,质量为m)从电场中的A点沿电场线所在的直线以速度v0开始运动,到达B点是时速度为零,电场线方向未知,求:
A、B两点间电势差UAB
 为多少?哪点电势高?
为多少?哪点电势高?电子从A点运动到B点所用时间为多少?
A、B两点间距离为多大?