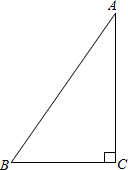
如图，在平面直角坐标系中，已知抛物线y＝－
x2＋bx＋c经过点A(0，1)、B（3，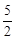
）两点，BC⊥x轴，垂足为C．点P是线段AB上的一动点（不与A，B重合），过点P作x轴的垂线交抛物线于点M，设点P的横坐标为t．
(1)求此抛物线的函数表达式；
(2)连结AM、BM，设△AMB的面积为S，求S关于t的函数关系式，并求出S的最大值；
(3)连结PC，当t为何值时，四边形PMBC是菱形．
如图，在单位长度为1的正方形网格中，一段圆弧经过网格的交点A、B、C。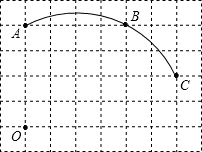
⑴请完成如下操作：①以点O为原点、竖直和水平方向为轴、网格边长为单位长，建立平面直角坐标系；②根据图形提供的信息，作出该圆弧所在圆的圆心D，并连接AD、CD。
⑵请在⑴的基础上，完成下列填空：
①写出点的坐标： C_______、D_______；
②直接写出⊙D半径＝_______（结果保留根号）；
③直接写出∠ADC＝_______；
④若扇形ADC是一个圆锥的侧面展开图，求该圆锥的底面的半径．
某商场销售一批书包，平均每天可售出40件，每件盈利20元。为了扩大售销，增加盈利，商场采取了降价措施。假设在一定范围内，书包的单价每降1元，商场平均每天可多售出2件。如果商场预计每 天通过销售这种书包盈利1200元， 那么书包应降价多少元？
如图AB是⊙O的直径，AP是⊙O的切线 ，A是切点，BP与⊙O交于点C. 若点D是AP中点，试证明直线CD是⊙O的切线.
如图，AB为⊙O的直径，AB=AC，BC交⊙O于点D，AC交⊙O于点E，∠BAC=45°．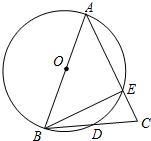
（1）求∠EBC的度数；
（2）求证：BD=CD．
已知△ABC中，∠C=90°，请利用尺规作出△ABC的内切圆O（不写 作法，请保留作图痕迹）