某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:
| 单价x(元) |
8 |
8.2 |
8.4 |
8.6 |
8.8 |
9 |
| 销量y (件 ) |
90 |
84 |
83 |
80 |
75 |
68 |
(I)求销量 与单价
与单价 间的回归直线方程;
间的回归直线方程;
(II)预计在今后的销售中,销量与单价仍然服从(I)中的关系,且该产品的成本是4元/件,为使工厂获得最大利润,该产品的单价应定为多少元?
已知等比数列{an}的前n项和为Sn,A1="3," 且3S1 , 2S2 , S3成等差数列.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=log3an,求Tn=b1b2 - b2b3 + b3b4 - b4b5 + … + b2n-1b2n - b2nb2n+1
已知函数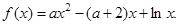
(Ⅰ)当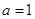 时,求曲线
时,求曲线 在点
在点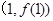 处的切线方程;
处的切线方程;
(Ⅱ)当 时,若
时,若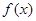 在区间
在区间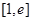 上的最小值为
上的最小值为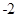 ,求
,求 的取值范围;
的取值范围;
(Ⅲ)若对任意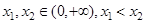 ,且
,且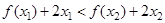 恒成立,求
恒成立,求 的取值范围.
的取值范围.
某服装厂生产一种服装,每件服装的成本为40元,出厂单价定为60元,该厂为鼓励销售商订购,决定当一次订购量超过100件时,每多订购一件,订购的全部服装的出场单价就降低0.02元,根据市场调查,销售商一次订购量不会超过600件.
(1)设一次订购x件,服装的实际出厂单价为p元,写出函数 的表达式;
的表达式;
(2)当销售商一次订购多少件服装时,该厂获得的利润最大?其最大利润是多少?
已知函数
(Ⅰ)求 的最小正周期
的最小正周期 ;(Ⅱ)求函数
;(Ⅱ)求函数 的单调递增区间;
的单调递增区间;
(Ⅲ)求函数 在区间
在区间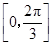 上的取值范围.
上的取值范围.
某生物技术公司研制出一种新流感疫苗,为测试该疫苗的有效性,公司选定2000个流感样本分成三组,测试结果如下表:
| A组 |
B组 |
C组 |
|
| 疫苗有效 |
 |
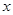 |
 |
| 疫苗无效 |
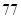 |
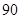 |
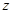 |
若在全体样本中随机抽取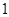 个,恰好抽到B组疫苗有效的概率是
个,恰好抽到B组疫苗有效的概率是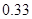 。
。
(Ⅰ)求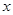 的值;
的值;
(II)现用分层抽样的方法在全体样本中抽取 个测试结果,问应在C组抽取多少个?
个测试结果,问应在C组抽取多少个?
(III)若疫苗有效的概率小于 ,则认为测试没有通过,已知
,则认为测试没有通过,已知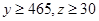 ,求这种新流感疫苗不能通过测试的概率。
,求这种新流感疫苗不能通过测试的概率。