(本小题12分) 
=（
）， 
=
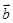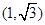，f（x）=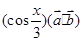
①求f(x)图象对称中心坐标
②若△ABC三边a、b、c满足b2=ac，且b边所对角为x，求x的范围及f（x）值域。
设椭圆的中心是坐标原点，长轴在x轴上，离心率e=
，已知点P（0，
）到椭圆上的点的最远距离是
，求这个椭圆方程。
中心在原点，一焦点为F1（0，5
）的椭圆被直线y=3x－2截得的弦的中点横坐标是
，求此椭圆的方程。
椭圆的一个顶点为A（2，0），其长轴长是短轴长的2倍，求椭圆的标准方程．
已知三角形
的两顶点为
，它的周长为
,求顶点
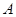轨迹方程．
设Ｐ，Ｑ，Ｒ，Ｓ四人分比获得１——４等奖，已知：
（１）若Ｐ得一等奖，则Ｑ得四等奖；
（２）若Ｑ得三等奖，则Ｐ得四等奖；
（３）Ｐ所得奖的等级高于Ｒ；
（４）若Ｓ未得一等奖，则Ｐ得二等奖；
（５）若Ｑ得二等奖，则Ｒ不是四等奖；
（６）若Ｑ得一等奖，则Ｒ得二等奖。
问Ｐ，Ｑ，Ｒ，Ｓ分别获得几等奖？