.已知向量 ,ω>0,记函数
,ω>0,记函数 =
= ,若
,若 的最小正周期为
的最小正周期为 .
.
⑴ 求ω的值;
⑵ 设△ABC的三边a、b、c满足b2=ac,且边b所对的角为 ,求
,求 的范围,
的范围,
并求此时函数 的值域。
的值域。
(本小题满分12分)
已知函数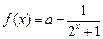 .;
.;
(1)确定 的值,使
的值,使 为奇函数;
为奇函数;
(2)当 为奇函数时,求
为奇函数时,求 的值域.
的值域.
(本小题满分12分)某产品按质量分为10个档次,生产第一档(即最低档次)的利润是每件8元,每提高一个档次,利润每件增加2元,但每提高一个档次,在相同的时间内,产量减少3件。如果在规定的时间内,最低档次的产品可生产60件
(I)请写出相同时间内产品的总利润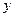 与档次
与档次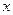 之间的函数关系式,并写出
之间的函数关系式,并写出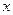 的定义域
的定义域
(II)在同样的时间内,生产哪一档次产品的总利润最大?并求出最大利润.
(本小题满分12分)已知函数
(1)判断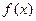 的奇偶性,并证明你的结论;
的奇偶性,并证明你的结论;
(2)证明:函数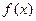 在
在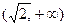 内是增函数
内是增函数
(本小题满分10分)
(1)计算: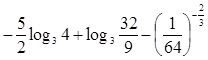
(2)已知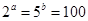 求
求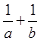 的值
的值
已知全集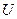 为
为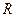 ,集合
,集合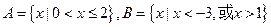
求:(1)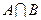 (2)
(2)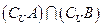 ;(3)
;(3)