有一个装有进出水管的容器,单位时间内进水管与出水管的进出水量均一定,已知容器的容积为600升,图中线段OA与BC,分别表示单独打开一个进水管和单独打开一个出水管时,容器的存水量Q(升)随时间t变化的函数关系.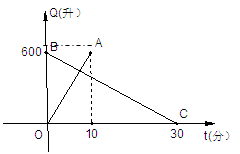
(1)求线段BC所表示的Q与t之间的函数关系式,并写出自变量t的取值范围;
(2)现已知容器内有水200升,先打开两个进水管和一个出水管一段时间,然后再关上一个进水管,直至把容器放满水,若总共用时不超过8分钟。请问,在这个过程中同时打开两个进水管和一个出水管的时间至少是多少分钟?
(本题8分)小敏上午8:00从家里出发,骑车去一家超市购物,然后从这家超市返回家中。小敏离家的路程 (米)和所经过的时间
(米)和所经过的时间 之间的函数图象如图所示。请根据图象回答下列问题:
之间的函数图象如图所示。请根据图象回答下列问题: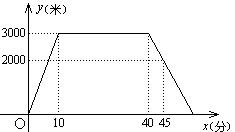
(1)小敏去超市途中的速度是多少?在超市逗留了多少时间?
(2)小敏几点几分返回到家?
(本题8分)
(1)计算: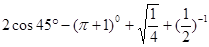 ;
;
(2)解不等式: ≤
≤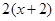
如图,在△ABC中,AB=5,AC=9,S△ABC= ,动点P从A点出发,沿射线AB方向以每秒5个单位的速度运动,动点Q从C点出发,以相同的速度在线段AC上由C向A运动,当Q点运动到A点时,P、Q两点同时停止运动,以PQ为边作正方形PQEF(P、Q、E、F按逆时针排序),以CQ为边在AC上方作正方形QCGH.
,动点P从A点出发,沿射线AB方向以每秒5个单位的速度运动,动点Q从C点出发,以相同的速度在线段AC上由C向A运动,当Q点运动到A点时,P、Q两点同时停止运动,以PQ为边作正方形PQEF(P、Q、E、F按逆时针排序),以CQ为边在AC上方作正方形QCGH.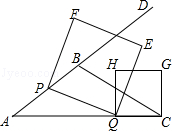
(1)求tanA的值;
(2)设点P运动时间为t,正方形PQEF的面积为S,请探究S是否存在最小值?若存在,求出这个最小值,若不存在,请说明理由;
(3)当t为何值时,正方形PQEF的某个顶点(Q点除外)落在正方形QCGH的边上,请直接写出t的值.
高铁的开通,给衢州市民出行带来了极大的方便,“五一”期间,乐乐和颖颖相约到杭州市的某游乐园游玩,乐乐乘私家车从衢州出发1小时后,颖颖乘坐高铁从衢州出发,先到杭州火车站,然后再转车出租车取游乐园(换车时间忽略不计),两人恰好同时到达游乐园,他们离开衢州的距离y(千米)与乘车时间t(小时)的关系如图所示.
请结合图象解决下面问题:
(1)高铁的平均速度是每小时多少千米?
(2)当颖颖达到杭州火车东站时,乐乐距离游乐园还有多少千米?
(3)若乐乐要提前18分钟到达游乐园,问私家车的速度必须达到多少千米/小时?
小明在课外学习时遇到这样一个问题:
定义:如果二次函数y=a1x2+b1x+c1(a1≠0,a1,b1,c1是常数)与y=a2x2+b2x+c2(a2≠0,a2,b2,c2是常数)满足a1+a2=0,b1=b2,c1+c2=0,则称这两个函数互为“旋转函数”.
求函数y=﹣x2+3x﹣2的“旋转函数”.
小明是这样思考的:由函数y=﹣x2+3x﹣2可知,a1=﹣1,b1=3,c1=﹣2,根据a1+a2=0,b1=b2,c1+c2=0,求出a2,b2,c2,就能确定这个函数的“旋转函数”.
请参考小明的方法解决下面问题:
(1)写出函数y=﹣x2+3x﹣2的“旋转函数”;
(2)若函数y=﹣x2+ mx﹣2与y=x2﹣2nx+n互为“旋转函数”,求(m+n)2015的值;
mx﹣2与y=x2﹣2nx+n互为“旋转函数”,求(m+n)2015的值;
(3)已知函数y=﹣ (x+1)(x﹣4)的图象与x轴交于点A、B两点,与y轴交于点C,点A、B、C关于原点的对称点分布是A1,B1,C1,试证明经过点A1,B1,C1的二次函数与函数y=﹣
(x+1)(x﹣4)的图象与x轴交于点A、B两点,与y轴交于点C,点A、B、C关于原点的对称点分布是A1,B1,C1,试证明经过点A1,B1,C1的二次函数与函数y=﹣ (x+1)(x﹣4)互为“旋转函数.”
(x+1)(x﹣4)互为“旋转函数.”