如图,⊙O的半径为6cm,将圆折叠,使点C与圆心O重合,折痕为AB,E、F是AB上两点(E、F不与A、B重合且E在F右边),且AF=BE.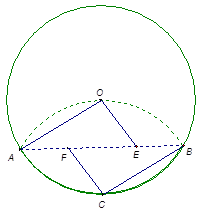
(1)判定四边形OECF的形状;
(2)AF为多少时,△CFB为直角三角形。
如图,已知∠BAP与∠APD互补,∠1=∠2,在括号中填上理由.
∵∠BAP与∠APD互补()
∴AB∥CD()
∴∠BAP=∠APC()
又∵∠1=∠2()
所以∠BAP-∠1=∠APC-∠2()
即∠3=∠4
∴AE∥PF()
∴∠E=∠F ( )
如图,△ABC在直角坐标系中,
(1)请写出△ABC各点的坐标。
(2)求出S△ABC
(3)若把△ABC向上平移2个单位,再向右平移2个单位得△A′B′C′,在图中画出△A′B′C′,并写出A′、B′、C′的坐标。
解方程:(1) =8
=8
(2) ="27"
="27"
如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.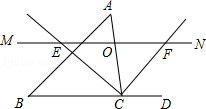
(1)求证:OE=OF;
(2)若CE=8,CF=6,求OC的长;
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
如图,在△ABC中,AB=AC,AD是△ABC的角平分线,作AE∥BC,CE∥AD,AE、CE交于点E.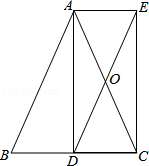
(1)证明:四边形ADCE是矩形.
(2)若DE交AC于点O,证明:OD∥AB且OD=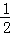 AB.
AB.